Examples using graph.asy of the Asymptote drawing software
graph-fig001

Show graph/fig0010.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis
size(8cm,0,false); import graph; xlimits(0, 200); ylimits(-50, 50); yaxis("y-value"); xaxis("x-value");
graph-fig002

Show graph/fig0020.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis
size(8cm,0,false); import graph; xlimits(0, 200); ylimits(-50, 50); yaxis( "y-value", Left); xaxis( "x-value", Bottom(true));
graph-fig003

Show graph/fig0030.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis
size(8cm,0,false); import graph; xlimits( -100, 100); ylimits( -50, 50); yaxis( "y" , RightTicks()); xaxis( "x", Ticks());
graph-fig004

Show graph/fig0040.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis
size(8cm,0); import graph; xlimits( -100, 100); ylimits( -50, 50); yaxis( "$y$" , Ticks(Label(currentpen+fontsize(8),align=E))); xaxis( "$x$", Ticks(Label(currentpen+fontsize(8))));
graph-fig005

Show graph/fig0050.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Defaultpen
size(8cm,0); import graph; xlimits( -100, 100); ylimits( -50, 50); defaultpen(overwrite(SuppressQuiet)); yaxis( "$y$" , Ticks(Label(.8red+fontsize(8),align=E)), p=.8red); xaxis( "$x$", Ticks(Label(.8blue+fontsize(8))), p=.8blue);
graph-fig006

Show graph/fig0060.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Grid
size(8cm,0); import graph; xlimits( -3pi, 3pi); ylimits( -5, 5); yaxis( "y" , LeftRight(), RightTicks(pTick=.8red, ptick=lightgrey, extend=true)); xaxis( "x-value", BottomTop(), Ticks(Label("$%.2f$",red), Step=2pi, step=pi/5, pTick=.8red, ptick=lightgrey, extend=true));
graph-fig007
Show graph/fig0070.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Number format
size(8cm,0); import graph; xlimits( -3pi, 3pi); xaxis(BottomTop(), Ticks(Label("$%.2f$",red), Step=2pi, step=pi/5, pTick=.8red));
graph-fig008
Show graph/fig0080.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Number format | #Tex/latex features
size(8cm,0); import graph; texpreamble("\usepackage[frenchb]{babel}"); xlimits( -3pi, 3pi); xaxis(BottomTop(), Ticks(Label("$\nombre{%.2f}$",red), Step=2pi, step=pi/5, pTick=.8red));
graph-fig009
Show graph/fig0090.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Number format | #Tex/latex features
size(8cm,0); import graph; texpreamble("\usepackage[frenchb]{babel}"); xlimits( -10000, 10000); xaxis(BottomTop(), Ticks(Label("$\nombre{%0.f}$",red), Step=5000, step=500, pTick=.8red));
graph-fig010
Show graph/fig0110.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Number format | #Tex/latex features
// An other solution... size(8cm,0); import graph; usepackage("icomma"); xlimits( -3pi, 3pi); xaxis(Ticks(Label(red), Step=2pi,step=pi/5,pTick=.8red));
graph-fig011

Show graph/fig0120.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label
size(6cm,0); import graph; xlimits( -3, 3); ylimits( -3, 3); xaxis(Ticks("%")); yaxis(Ticks("%")); labelx(1,2S); labely(1,2W); labelx("$O$",0,SW); dot((0,0));
graph-fig012

Show graph/fig0130.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label
import graph; unitsize(x=1cm); real f(real x){return x;} xlimits( -3, 3); ylimits( -3, 3); draw(graph(f,-3,3)); xaxis(Label("$x$",position=EndPoint, align=SE),Ticks("%",extend=true), Arrow); yaxis(Label("$y$",position=EndPoint, align=NW),Ticks("%",extend=true), Arrow); labelx(1,2S); labely(1,2W); labelx("$O$",0,SE); dot((0,0));
graph-fig013

Show graph/fig0140.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label
unitsize(x=1cm); import graph; xlimits( -3, 2); ylimits( -3, 3); xaxis(xmin=-3, xmax=2,Ticks("%")); yaxis(ymin=-3, ymax=3, Ticks("%")); labelx(1,2S); labely(1,2W); labelx("$O$",0,SW); dot((0,0)); draw(Label("$x$",position=Relative(1),align=2S),(currentpicture.userMin().x-1,0)--(currentpicture.userMax().x+1,0),Arrow); draw(Label("$y$",position=Relative(1),align=2W),(0,currentpicture.userMin().y-1)--(0,currentpicture.userMax().y+1),Arrow);
graph-fig014

Show graph/fig0150.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label
import graph; unitsize(1cm); xlimits( -3, 2); ylimits( -3, 3); xaxis("$x$",Ticks("%",begin=false, end=false),arrow=Arrow); yaxis("$y$",Ticks("%",begin=false, end=false),arrow=Arrow); labelx(1,2S); labely(1,2W); labelx("$O$",0,SW); dot((0,0));
graph-fig015

Show graph/fig0160.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label
import graph; unitsize(1cm); xlimits( -3, 2); ylimits( -3, 3); xaxis("$x$",Ticks(ticklabel=NoZeroFormat,1bp+red,end=false),arrow=Arrow); yaxis("$y$",Ticks(ticklabel=NoZeroFormat,1bp+red,end=false),arrow=Arrow); labelx(scale(.75)*"$O$",0,SW);
graph-fig016

Show graph/fig0170.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label
import graph; unitsize(1cm); xlimits( -3, 2); ylimits( -3, 3); xaxis("$x$",Ticks(modify=NoZero,1bp+red,end=false),arrow=Arrow); yaxis("$y$",Ticks(modify=NoZero,1bp+red,end=false),arrow=Arrow); labelx(scale(.75)*"$O$",0,SW);
graph-fig017

Show graph/fig0180.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label
import graph; unitsize(1cm); xlimits( -3, 2); ylimits( -3, 3); xaxis("$x$", Ticks(ticklabel=OmitFormat(-2,-1,2), modify=NoZero, 1bp+red, end=false), arrow=Arrow); yaxis("$y$", Ticks(ticklabel=OmitFormat(-2,-1,2,3), modify=NoZero, 1bp+red, end=false), arrow=Arrow); labelx(scale(.75)*"$O$",0,SW);
graph-fig018

Show graph/fig0190.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label | #Grid
import graph; unitsize(x=1cm, y=1.5cm); xlimits( -3, 2); ylimits( -2, 2); xaxis(BottomTop, Ticks("%",extend=true, ptick=lightgrey)); yaxis(LeftRight, Ticks("%",extend=true, ptick=lightgrey)); xequals(Label("$y$",align=2NW),0,ymin=-2.5, ymax=2.5, p=linewidth(1.5pt), Arrow(2mm)); yequals(Label("$x$",align=2SE),0,xmin=-3.5, xmax=2.5, p=linewidth(1.5pt), Arrow(2mm)); labelx(Label("$1$",UnFill), 1); labely(Label("$1$",UnFill), 1); labelx("$O$",0,SW); dot((0,0));
graph-fig019

Show graph/fig0200.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Axis | #Label | #Grid | #Vector
import graph; void graphicrules(picture pic=currentpicture, string prefix=defaultfilename, real unit=1cm, real xunit=unit != 0 ? unit : 0, real yunit=unit != 0 ? unit : 0, real xmin, real xmax, real ymin, real ymax) { xlimits(xmin, xmax); ylimits(ymin, ymax); unitsize(x=xunit, y=yunit); } void grid(picture pic=currentpicture, real xmin=pic.userMin().x, real xmax=pic.userMax().x, real ymin=pic.userMin().y, real ymax=pic.userMax().y, real xStep=1, real xstep=.5, real yStep=1, real ystep=.5, pen pTick=nullpen, pen ptick=grey, bool above=false) { draw(pic,box((xmin,ymin),(xmax,ymax)),invisible); xaxis(pic, BottomTop, xmin, xmax, Ticks("%",extend=true,Step=xStep,step=xstep,pTick=pTick,ptick=ptick), above=above); yaxis(pic, LeftRight, ymin, ymax, Ticks("%",extend=true,Step=yStep,step=ystep,pTick=pTick,ptick=ptick), above=above); } void cartesianaxis(picture pic=currentpicture, Label Lx=Label("$x$",align=S), Label Ly=Label("$y$",align=W), real xmin=pic.userMin().x, real xmax=pic.userMax().x, real ymin=pic.userMin().y, real ymax=pic.userMax().y, real extrawidth=1, real extraheight=extrawidth, pen p=currentpen, ticks xticks=Ticks("%",pTick=nullpen, ptick=grey), ticks yticks=Ticks("%",pTick=nullpen, ptick=grey), bool above=true, arrowbar arrow=Arrow) { extraheight= cm*extraheight/(2*pic.yunitsize); extrawidth = cm*extrawidth/(2*pic.xunitsize); yequals(pic, Lx, 0, xmin-extrawidth, xmax+extrawidth, p, above, arrow=arrow); xequals(pic, Ly, 0, ymin-extraheight, ymax+extraheight, p, above, arrow=arrow); yequals(pic, 0, xmin, xmax, p, xticks, above); xequals(pic, 0, ymin, ymax, p, yticks, above); } void labeloij(picture pic=currentpicture, Label Lo=Label("$O$",NoFill), Label Li=Label("$\vec{\imath}$",NoFill), Label Lj=Label("$\vec{\jmath}$",NoFill), pair diro=SW, pair diri=S, pair dirj=W, pen p=scale(2)*currentpen, filltype filltype=NoFill, arrowbar arrow=Arrow(2mm)) { if (Lo.filltype==NoFill) Lo.filltype=filltype; if (Li.filltype==NoFill) Li.filltype=filltype; if (Lj.filltype==NoFill) Lj.filltype=filltype; labelx(pic, Lo, 0, diro, p); draw(pic, Li, (0,0)--(1,0), diri, p, arrow); draw(pic, Lj, (0,0)--(0,1), dirj, p, arrow); dot(pic, (0,0), dotsize(p)+p); } //The figure starts here graphicrules(yunit=1.5cm, xmin=-3, xmax=3, ymin=-2, ymax=2); grid(); cartesianaxis(arrow=None); labeloij(UnFill);
graph-fig020

Show graph/fig0210.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Grid
import graph; void graphicrules(picture pic=currentpicture, real unit=1cm, real xunit=unit != 0 ? unit : 0, real yunit=unit != 0 ? unit : 0, real xmin, real xmax, real ymin, real ymax) { xlimits(xmin, xmax); ylimits(ymin, ymax); pic.unitsize(x=xunit,y=yunit); } picture millimeterpaper(picture pic=currentpicture, pair O=(0,0), real xmin=infinity, real xmax=infinity, real ymin=infinity, real ymax=infinity, pen p=.5bp+orange) { picture opic; real cofx=pic.xunitsize/cm, cofy=pic.yunitsize/cm; real xmin= (xmin == infinity) ? pic.userMin().x*cofx : xmin*cofx, xmax= (xmax == infinity) ? pic.userMax().x*cofx : xmax*cofx, ymin= (ymin == infinity) ? pic.userMin().y*cofy : ymin*cofy, ymax= (ymax == infinity) ? pic.userMax().y*cofy : ymax*cofy; path ph=(xmin*cm,0)--(xmax*cm,0), pv=(0,ymin*cm)--(0,ymax*cm); real [] step={5, 1, .5, .1}; pen [] p_={ p, scale(.7)*p, scale(.4)*p, scale(.2)*p}; for (int j=0; j<4; ++j) { for (real i=O.y; i<= ymax; i+=step[j]) draw(opic, shift(0,i*cm)*ph, p_[j]); for (real i=O.y; i>=ymin ; i-=step[j]) draw(opic, shift(0,i*cm)*ph, p_[j]); for (real i=O.x; i<=xmax; i+=step[j]) draw(opic, shift(i*cm,0)*pv, p_[j]); for (real i=O.x; i>=xmin; i-=step[j]) draw(opic, shift(i*cm,0)*pv, p_[j]); } return opic; } graphicrules(xunit=2cm, yunit=1.5cm, xmin=-3, xmax=2, ymin=-2, ymax=2); add(millimeterpaper(p=3bp+orange),(0,0)); xaxis(xmin=-3, xmax=2, Ticks("%")); yaxis(ymin=-2, ymax=2, Ticks("%")); xequals(Label("$y$",align=2NW),0,ymin=-2.25, ymax=2.25, p=linewidth(1.5pt), Arrow(2mm)); yequals(Label("$x$",align=2SE),0,xmin=-3.25, xmax=2.25, p=linewidth(1.5pt), Arrow(2mm)); labelx(Label("$1$",UnFill), 1); labely(Label("$1$",UnFill), 1); labelx("$O$",0,SW); dot((0,0));
graph-fig021

Show graph/fig0220.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Buildcycle | #Pattern | #Tex/latex features | #Grid
import graph; import patterns; usepackage("mathrsfs"); unitsize(2cm,1.5cm); real xmin=-1,xmax=4; real ymin=-1,ymax=5; // Definition of fonctions f and g : real f(real x) {return 4x-x^2+4/(x^2+1)^2;} real g(real x) {return x-1+4/(x^2+1)^2;} // Trace the curves : path Cf=graph(f,xmin,xmax,n=400); path Cg=graph(g,xmin,xmax,n=400); draw(Cf,linewidth(1bp)); draw(Cg,linewidth(1bp)); xlimits(xmin,xmax,Crop); ylimits(ymin,ymax,Crop); // The grid : xaxis(BottomTop, xmin, xmax, Ticks("%", Step=1, step=0.5, extend=true, ptick=lightgrey)); yaxis(LeftRight, ymin, ymax, Ticks("%", Step=1, step=0.5, extend=true, ptick=lightgrey)); // The axis. xequals(Label("$y$",align=W),0,ymin=ymin-0.25, ymax=ymax+0.25, Ticks(NoZero,pTick=nullpen, ptick=grey), p=linewidth(1pt), Arrow(2mm)); yequals(Label("$x$",align=S),0,xmin=xmin-0.25, xmax=xmax+0.25, Ticks(NoZero,pTick=nullpen, ptick=grey), p=linewidth(1pt), Arrow(2mm)); labelx(Label("$O$",NoFill), 0, SW); draw(Label("$\vec{\imath}$",align=S,UnFill), (0,0)--(1,0),scale(2)*currentpen,Arrow); draw(Label("$\vec{\jmath}$",align=W,UnFill), (0,0)--(0,1),scale(2)*currentpen,Arrow); dot((0,0)); label("$\mathscr{C}_f$",(2.25,f(2.25)),2N); label("$\mathscr{C}_f$",(2.25,g(2.25)),2S); // Les hachures. path vline=(1,-1)--(1,5); add("hachure",hatch(3mm)); fill(buildcycle(vline,graph(f,1,4),graph(g,1,4)),pattern("hachure"));
graph-fig022

Show graph/fig0230.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Fraction | #Label | #Tex/latex features | #Struct
import graph; unitsize(x=1cm,y=2cm); struct rational { int p; int q; real ep=1/10^5; }; rational operator init() {return new rational;} rational rational(real x, real ep=1/10^5) { rational orat; int q=1; while (abs(round(q*x)-q*x)>ep) { ++q; } orat.p=round(q*x); orat.q=q; orat.ep=ep; return orat; } int pgcd(int a, int b) { int a_=abs(a), b_=abs(b), r=a_; if (b_>a_) {a_=b_; b_=r; r=a_;} while (r>0) { r=a_%b_; a_=b_; b_=r; } return a_; } string texfrac(int p, int q, string factor="", bool signin=false, bool factorin=true, bool displaystyle=false, bool zero=true) { if (p==0) return (zero ? "$0$" : ""); string disp= displaystyle ? "$\displaystyle " : "$"; int pgcd=pgcd(p,q); int num= round(p/pgcd), den= round(q/pgcd); string nums; if (num==1) if (factor=="" || (!factorin && (den !=1))) nums="1"; else nums=""; else if (num==-1) if (factor=="" || (!factorin && (den !=1))) nums="-1"; else nums="-"; else nums= (string) num; if (den==1) return "$" + nums + factor + "$"; else { string dens= (den==1) ? "" : (string) den; if (signin || num>0) if (factorin) return disp + "\frac{" + nums + factor + "}{" + (string) dens + "}$"; else return disp + "\frac{" + nums + "}{" + (string) dens + "}"+ factor + "$"; else { if (num==-1) if (factor=="" || !factorin) nums="1"; else nums=""; else nums=(string)(abs(num)); if (factorin) return disp + "-\frac{" + nums + factor + "}{" + (string) dens + "}$"; else return disp + "-\frac{" + nums + "}{" + (string) dens + "}"+ factor + "$"; } } } string texfrac(rational x, string factor="", bool signin=false, bool factorin=true, bool displaystyle=false, bool zero=true) { return texfrac(x.p, x.q, factor, signin, factorin, displaystyle, zero); } ticklabel labelfrac(real ep=1/10^5, real factor=1.0, string symbol="", bool signin=false, bool symbolin=true, bool displaystyle=false, bool zero=true) { return new string(real x) { return texfrac(rational(x/factor), symbol, signin, symbolin, displaystyle, zero); }; } ticklabel labelfrac=labelfrac(); xlimits( -2pi, 2pi); ylimits( -1, 1); yaxis("y",LeftRight , Ticks(labelfrac,Step=.5,step=.25, ptick=grey, extend=true)); xaxis("$\theta$",BottomTop, Ticks(labelfrac(factor=pi,symbol="\pi",symbolin=false), Step=pi/2, step=pi/4, ptick=grey, extend=true)); draw(graph(new real(real x){return sin(x);},-2pi,2pi)); draw(graph(new real(real x){return cos(x);},-2pi,2pi), .8red);
graph-fig023

Show graph/fig0240.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Fraction | #Label | #Tex/latex features | #Struct
import graph; // public real xunit=1cm,yunit=1cm; void graphicrules(picture pic=currentpicture, string prefix=defaultfilename, real unit=1cm, real xunit=unit != 0 ? unit : 0, real yunit=unit != 0 ? unit : 0, real xmin, real xmax, real ymin, real ymax) { xlimits(xmin, xmax); ylimits(ymin, ymax); unitsize(x=xunit, y=yunit); } struct rational { int p; int q; real ep=1/10^5; }; rational operator init() {return new rational;} rational rational(real x, real ep=1/10^5) { rational orat; int q=1; while (abs(round(q*x)-q*x)>ep) { ++q; } orat.p=round(q*x); orat.q=q; orat.ep=ep; return orat; } int pgcd(int a, int b) { int a_=abs(a), b_=abs(b), r=a_; if (b_>a_) {a_=b_; b_=r; r=a_;} while (r>0) { r=a_%b_; a_=b_; b_=r; } return a_; } string texfrac(int p, int q, string factor="", bool signin=false, bool factorin=true, bool displaystyle=false, bool zero=true) { if (p==0) return (zero ? "$0$" : ""); string disp= displaystyle ? "$\displaystyle " : "$"; int pgcd=pgcd(p,q); int num= round(p/pgcd), den= round(q/pgcd); string nums; if (num==1) if (factor=="" || (!factorin && (den !=1))) nums="1"; else nums=""; else if (num==-1) if (factor=="" || (!factorin && (den !=1))) nums="-1"; else nums="-"; else nums= (string) num; if (den==1) return "$" + nums + factor + "$"; else { string dens= (den==1) ? "" : (string) den; if (signin || num>0) if (factorin) return disp + "\frac{" + nums + factor + "}{" + (string) dens + "}$"; else return disp + "\frac{" + nums + "}{" + (string) dens + "}"+ factor + "$"; else { if (num==-1) if (factor=="" || !factorin) nums="1"; else nums=""; else nums=(string)(abs(num)); if (factorin) return disp + "-\frac{" + nums + factor + "}{" + (string) dens + "}$"; else return disp + "-\frac{" + nums + "}{" + (string) dens + "}"+ factor + "$"; } } } string texfrac(rational x, string factor="", bool signin=false, bool factorin=true, bool displaystyle=false, bool zero=true) { return texfrac(x.p, x.q, factor, signin, factorin, displaystyle, zero); } ticklabel labelfrac(real ep=1/10^5, real factor=1.0, string symbol="", bool signin=false, bool symbolin=true, bool displaystyle=false, bool zero=true) { return new string(real x) { return texfrac(rational(x/factor), symbol, signin, symbolin, displaystyle, zero); }; } ticklabel labelfrac=labelfrac(); void grid(picture pic=currentpicture, real xmin=pic.userMin().x, real xmax=pic.userMax().x, real ymin=pic.userMin().y, real ymax=pic.userMax().y, real xStep=1, real xstep=.5, real yStep=1, real ystep=.5, pen pTick=nullpen, pen ptick=grey, bool above=true) { xaxis(pic, BottomTop, xmin, xmax, Ticks("%",extend=true,Step=xStep,step=xstep,pTick=pTick,ptick=ptick), above=above); yaxis(pic, LeftRight, ymin, ymax, Ticks("%",extend=true,Step=yStep,step=ystep,pTick=pTick,ptick=ptick), above=above); } void cartesianaxis(picture pic=currentpicture, Label Lx=Label("$x$",align=S), Label Ly=Label("$y$",align=W), real xmin=pic.userMin().x, real xmax=pic.userMax().x, real ymin=pic.userMin().y, real ymax=pic.userMax().y, real extrawidth=1, real extraheight=extrawidth, pen p=currentpen, ticks xticks=Ticks("%",pTick=nullpen, ptick=grey), ticks yticks=Ticks("%",pTick=nullpen, ptick=grey), bool above=true, arrowbar arrow=Arrow) { extraheight= cm*extraheight/(2*pic.yunitsize); extrawidth = cm*extrawidth/(2*pic.xunitsize); yequals(pic, Lx, 0, xmin-extrawidth, xmax+extrawidth, p, above, arrow=arrow); yequals(pic, 0, xmin, xmax, p, xticks, above); xequals(pic, Ly, 0, ymin-extraheight, ymax+extraheight, p, above, arrow=arrow); xequals(pic, 0, ymin, ymax, p, yticks, above); } void labeloij(picture pic=currentpicture, Label Lo=Label("$O$",NoFill), Label Li=Label("$\vec{\imath}$",NoFill), Label Lj=Label("$\vec{\jmath}$",NoFill), pair diro=SW, pair diri=S, pair dirj=W, pen p=scale(2)*currentpen, filltype filltype=NoFill, arrowbar arrow=Arrow(2mm)) { if (Lo.filltype==NoFill) Lo.filltype=filltype; if (Li.filltype==NoFill) Li.filltype=filltype; if (Lj.filltype==NoFill) Lj.filltype=filltype; labelx(pic, Lo, 0, diro, p); draw(pic, Li, (0,0)--(1,0), diri, p, arrow); draw(pic, Lj, (0,0)--(0,1), dirj, p, arrow); dot(pic, (0,0), dotsize(p)+p); } void labeloIJ(picture pic=currentpicture, Label Lo=Label("$O$",NoFill), Label LI=Label("$I$",NoFill), Label LJ=Label("$J$",NoFill), pair diro=SW, pair dirI=S, pair dirJ=W, pen p=currentpen, filltype filltype=NoFill, arrowbar arrow=Arrow) { if (Lo.filltype==NoFill) Lo.filltype=filltype; if (LI.filltype==NoFill) LI.filltype=filltype; if (LJ.filltype==NoFill) LJ.filltype=filltype; labelx(pic, LI, 1, dirI, p); labely(pic, LJ, 1, dirJ, p); labelx(pic, Lo, 0, diro, p); dot(pic, (0,0), dotsize(p)+p); } graphicrules(xunit=1cm, yunit=3cm, xmin=-2pi, xmax=2pi, ymin=-1, ymax=1); grid(xStep=pi/2, xstep=pi/4, yStep=.5, ystep=.25); cartesianaxis(xticks=Ticks(Label(UnFill),labelfrac(factor=pi,symbol="\pi",symbolin=true, zero=false),Step=pi/2, step=pi/4, ptick=grey), yticks=Ticks(Label(UnFill),labelfrac(zero=false),Step=.5,step=.25, ptick=grey), arrow=None); dot("$O$",(0,0),2SW);
graph-fig024

Show graph/fig0250.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Hyperbola | #Contour | #Function (implicit)
size(10cm,0); import contour; import graph; xlimits( -3, 3); ylimits( -3, 3); yaxis( "$y$" , Ticks()); xaxis( "$x$", Ticks()); real f(real x, real y) {return x*y;} draw(contour(f,(-3,-3),(3,3),new real[] {1}));
graph-fig025

Show graph/fig0260.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Hyperbola | #Contour | #Function (implicit) | #Array
size(10cm,0); import contour; import stats; import graph; xlimits( -5, 5); ylimits( -4, 5); yaxis( "$y$" , Ticks(Label(currentpen+fontsize(8),align=E))); xaxis( "$x$", Ticks(Label(currentpen+fontsize(8)))); real f(real x, real y) {return x^2-x-y^2+3y-6;} int min=-5, max=5, n=max-min+1; real[] value=sequence(min,max); pen[] p=sequence(new pen(int i) { return (value[i] >= 0 ? solid : dashed) + (value[i] >= 0 ? (value[i]/max)*red : (value[i]/min)*blue) + fontsize(4); },n); Label[] Labels=sequence(new Label(int i) { return Label(value[i] != 0 ? (string) value[i] : "",Relative(unitrand()),(0,0), UnFill(1bp)); },n); draw(Labels,contour(f,(-5,-5),(5,5),value),p);
graph-fig026

Show graph/fig0270.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Legend
//Author: John Bowman import graph; size(250,200,IgnoreAspect); real Sin(real t, real w) {return sin(w*t);} draw(graph(new real(real t) {return Sin(t,pi);},0,1),blue,"$\sin(\pi x)$"); draw(graph(new real(real t) {return Sin(t,2pi);},0,1),red,"$\sin(2\pi x)$"); xaxis("$x$",BottomTop,Ticks); yaxis("$y$",LeftRight,Ticks); attach(legend(),point(E),20E,UnFill);
graph-fig027

Show graph/fig0280.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Legend | #Typedef | #Tex/latex features
import graph; size(10cm,6cm,IgnoreAspect); typedef real realfcn(real); realfcn F(real p){ return new real(real x){return sin(x)/sqrt(p);}; }; real pmax=5; for (real p=1; p<=pmax; p+=1) { draw(graph(F(p),-2pi,2pi), ((p-1)/(pmax-1)*blue+(1-(p-1)/(pmax-1))*red), "$\frac{\sin(x)}{\sqrt{" + (string) p +"}}$"); } xlimits(-2pi,2pi); ylimits(-1,1); xaxis("$x$",BottomTop,Ticks); yaxis("$y$",LeftRight,Ticks); attach(legend(),point(E),20E,UnFill);
graph-fig028
Show graph/fig0290.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Interpolate | #Function (drawing) | #Legend | #Typedef
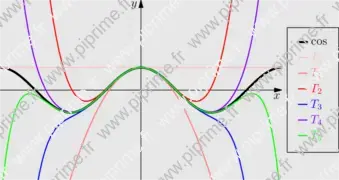
import graph; size(10cm); xaxis("$x$", -2*pi,2*pi, Arrow); yaxis("$y$", -4,4, Arrow); typedef real realfcn(real); // Define new type: real function of real realfcn TPC(int n) { //Return Taylor polynomial (degrees 2*n) of cos return new real(real x) { return sum(sequence(new real(int m){return (-1)^m*x^(2*m)/gamma(2*m+1);}, n+1)); }; } draw(graph(cos,-2pi,2pi), linewidth(2bp), legend="$\cos$"); int n=6; // Number of curves pen[] p={palered, lightred, red, blue, purple, green}; p.cyclic=true; // p[6]=p[0], p[7]=p[1], etc... for (int i=0; i < n; ++i) { draw(graph(TPC(i),-2*pi,2*pi), bp+p[i], legend="$T_{"+(string)i+"}$"); } xlimits(-2*pi,2*pi, Crop); ylimits(-4,4, Crop); attach(legend(linelength=3mm),point(E),5E); shipout(bbox(Fill(lightgrey)));
graph-fig029
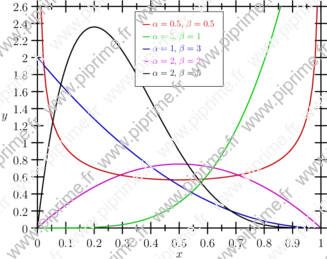
Beta distribution.
Show graph/fig0300.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Legend | #Typedef
import graph; unitsize(10cm,3cm); typedef real realfcn(real); realfcn betaFunction(real alpha, real beta){ return new real(real x){ return gamma(alpha+beta)/(gamma(alpha)+gamma(beta))*x^(alpha-1)*(1-x)^(beta-1); }; }; real[][] ab=new real[][] {{0.5,0.5},{5,1},{1,3},{2,2},{2,5}}; pen[] p=new pen[] {0.8*red, 0.8*green, 0.8*blue, 0.8*magenta, black}; for (int i=0; i < 5; ++i) { draw(graph(betaFunction(ab[i][0],ab[i][1]),1e-5,1-1e-5), bp+p[i], legend="$\alpha="+(string)ab[i][0]+",\;\beta="+(string)ab[i][1]+"$"); } xlimits(0,1,Crop); ylimits(0,2.6,Crop); xaxis("$x$",BottomTop,linewidth(bp),Ticks); yaxis("$y$",LeftRight,linewidth(bp),Ticks(Step=0.2)); attach(scale(0.75)*legend(linelength=3mm),point(N),5S,UnFill);
graph-fig030

Other examples of interpolations can be found here.
Show graph/fig0310.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Interpolate | #Function (drawing) | #Legend | #Typedef
import graph; unitsize(1cm); typedef real hermite(real); /** * Retourne la fonction polynôme de Hermite * passant par les points m(x_i,y_i) de nombre dérivée d_i en ce point. * Return Hermite polynomial interpolation function * passing by the points m (x_i, y_i) of derived number d_i in this point. **/ hermite hermite(pair [] m, real [] d) { return new real(real x){ int n=m.length; if (n != d.length) abort("Hermite: nombres de paramètres incorrectes."); real q,qk,s,y=0; for (int k=0; k<n ; ++k) { real q=1, qk=1, s=0; for (int j=0; j<n; ++j) { if (j!=k){ q=q*(x-m[j].x)^2; qk=qk*(m[k].x-m[j].x)^2; s=s+1/(m[k].x-m[j].x); } } y=y+q/qk*(m[k].y+(x-m[k].x)*(d[k]-2*s*m[k].y)); } return y; }; } pair[] m; real[] d; int nbpt=5; real xmin=-2pi, xmax=2pi, l=xmax-xmin, step=l/(nbpt+1); for (int i=1; i<=nbpt; ++i) { real x=xmin+i*step; m.push((x,sin(x))); draw(m[m.length-1],linewidth(2mm)); d.push(cos(x)); } xlimits(-2pi,2pi); ylimits(-2,2); xaxis("$x$",BottomTop,Ticks); yaxis("$y$",LeftRight,Ticks); draw(graph(sin,xmin,xmax),1mm+.8red,"$x\longmapsto{}\sin x$"); draw(graph(hermite(m,d),xmin,xmax),"$x\longmapsto{}H(x)$"); attach(legend(),point(10S),30S);
graph-fig031

Show graph/fig0320.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Interpolate | #Function (drawing) | #Legend
import graph; import interpolate; size(15cm,10cm,IgnoreAspect); real[] xpt,ypt; real [] xpt={1, 2, 4, 5, 7, 8, 10}; real [] ypt={1, 2, 2, 3, 1, 0.5, 3}; horner h=diffdiv(xpt,ypt); fhorner L=fhorner(h); scale(false,true); pen p=linewidth(1); draw(graph(L,min(xpt),max(xpt)),dashed+black+p,"Lagrange interpolation"); draw(graph(xpt,ypt,Hermite(natural)),red+p,"natural spline"); draw(graph(xpt,ypt,Hermite(monotonic)),blue+p,"monotone spline"); xaxis("$x$",BottomTop,LeftTicks(Step=1,step=0.25)); yaxis("$y$",LeftRight,RightTicks(Step=5)); dot(pairs(xpt,ypt),4bp+0.7black); attach(legend(),point(10S),30S);
graph-fig032

Show graph/fig0330.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Legend | #Tex/latex features | #Slopefield
import slopefield; import graph; size(8cm,0); real f(real t) {return exp(-t^2);} defaultpen(); xlimits( 0,1); ylimits( 0,1); yaxis( "$y$" ,LeftRight, RightTicks); xaxis( "$x$", Ticks()); draw(graph(f,0,1),"$x\longmapsto{}e^{-x^2}$"); draw(curve((0,0),f,(0,0),(1,10)),linecap(0)+red,"$\displaystyle x\longmapsto\int_{0}^{x}e^{-t^2}\;dt$"); //Test with three values calculated with Maxima: dot((.25,0.13816319508411845*sqrt(pi))^^(.5 , 0.26024993890652326*sqrt(pi))); dot((.75, 0.3555778168267576*sqrt(pi))); attach(legend(),point(10S),30S);
graph-fig033
Show graph/fig0340.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Font | #Axis
//Author: John Bowman import graph; size(2cm, 0); xlimits(0, 100); ylimits(-50, 50); yaxis( "y-value" ,Left, Courier("m", "n") + fontsize(12), RightTicks("%.4g"));
graph-fig034

Show graph/fig0350.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Align | #Picture | #Transform/scale/shift/rotate/projection
// From Asymptote's FAQ import graph; real width=15cm; real aspect=0.3; picture pic1,pic2; size(pic1,width,aspect*width,IgnoreAspect); size(pic2,width,aspect*width,IgnoreAspect); scale(pic1,false); scale(pic2,false); real xmin1=6; real xmax1=9; real xmin2=8; real xmax2=16; real a1=1; real a2=0.001; real f1(real x) {return a1*sin(x/2*pi);} real f2(real x) {return a2*sin(x/4*pi);} draw(pic1,graph(pic1,f1,xmin1,xmax1)); draw(pic2,graph(pic2,f2,xmin2,xmax2)); xaxis(pic1,Bottom,LeftTicks()); yaxis(pic1,"$f_1(x)$",Left,RightTicks); xaxis(pic2,Bottom,LeftTicks(Step=4)); yaxis(pic2,"$f_2(x)$",Left,RightTicks); yequals(pic1,0,Dotted); yequals(pic2,0,Dotted); pair min1=point(pic1,SW); pair max1=point(pic1,NE); pair min2=point(pic2,SW); pair max2=point(pic2,NE); real scale=(max1.x-min1.x)/(max2.x-min2.x); real shift=min1.x/scale-min2.x; transform t1 = pic1.calculateTransform(); transform t2 = pic2.calculateTransform(); transform T=xscale(scale*t1.xx)*yscale(t2.yy); add(pic1.fit()); real height=truepoint(N).y-truepoint(S).y; add(shift(0,-height)*(shift(shift)*pic2).fit(T));