Asymptote Gallery Tagged by “Typedef” #144
animations-fig009
Show animations/fig0100.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Animation
Tags : #Physics | #Graph | #Typedef | #Function (graphing) | #Animation
import animation; import graph; settings.tex="pdflatex"; settings.outformat="pdf"; unitsize(x=2cm,y=1.5cm); typedef real realfcn(real); real lambda=4; real T=2; real [] k=new real[3]; real [] w=new real[3]; k[0]=2pi/lambda; w[0]=2pi/T; real dk=-.5; k[1]=k[0]-dk; k[2]=k[0]+dk; real dw=1; w[1]=w[0]-dw; w[2]=w[0]+dw; real vp=w[1]/k[1]; real vg=dw/dk; realfcn F(real x) { return new real(real t) { return cos(k[1]*x-w[1]*t)+cos(k[2]*x-w[2]*t); }; }; realfcn G(real x) { return new real(real t) { return 2*cos(0.5*(k[2]-k[1])*x+0.5*(w[1]-w[2])*t); }; }; realfcn operator -(realfcn f) {return new real(real t) {return -f(t);};}; animation A; real tmax=abs(2pi/dk); real xmax=abs(2pi/dw); pen envelope=0.8*blue; pen fillpen=lightgrey; int n=50; real step=tmax/(n-1); for(int i=0; i < n; ++i) { save(); real t=i*step; real a=xmax*t/tmax-xmax/pi; real b=xmax*t/tmax; path f=graph(F(t),a,b); path g=graph(G(t),a,b); path h=graph(-G(t),a,b); fill(buildcycle(reverse(f),g),fillpen); draw(f); draw(g,envelope); draw(h,envelope); A.add(); restore(); } for(int i=0; i < n; ++i) { save(); real t=i*step; real a=-xmax/pi; real b=xmax; path f=graph(F(t),a,b); path g=graph(G(t),a,b); path h=graph(-G(t),a,b); path B=box((-xmax/pi,-2),(xmax,2)); fill(buildcycle(reverse(f),g,B),fillpen); fill(buildcycle(f,g,reverse(B)),fillpen); draw(f); draw(g,envelope); draw(h,envelope); A.add(); restore(); } A.movie();
graph-fig027

Show graph/fig0280.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Legend | #Typedef | #Tex/latex features
import graph; size(10cm,6cm,IgnoreAspect); typedef real realfcn(real); realfcn F(real p){ return new real(real x){return sin(x)/sqrt(p);}; }; real pmax=5; for (real p=1; p<=pmax; p+=1) { draw(graph(F(p),-2pi,2pi), ((p-1)/(pmax-1)*blue+(1-(p-1)/(pmax-1))*red), "$\frac{\sin(x)}{\sqrt{" + (string) p +"}}$"); } xlimits(-2pi,2pi); ylimits(-1,1); xaxis("$x$",BottomTop,Ticks); yaxis("$y$",LeftRight,Ticks); attach(legend(),point(E),20E,UnFill);
graph-fig028
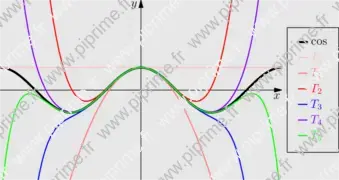
Show graph/fig0290.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Interpolate | #Function (drawing) | #Legend | #Typedef
import graph; size(10cm); xaxis("$x$", -2*pi,2*pi, Arrow); yaxis("$y$", -4,4, Arrow); typedef real realfcn(real); // Define new type: real function of real realfcn TPC(int n) { //Return Taylor polynomial (degrees 2*n) of cos return new real(real x) { return sum(sequence(new real(int m){return (-1)^m*x^(2*m)/gamma(2*m+1);}, n+1)); }; } draw(graph(cos,-2pi,2pi), linewidth(2bp), legend="$\cos$"); int n=6; // Number of curves pen[] p={palered, lightred, red, blue, purple, green}; p.cyclic=true; // p[6]=p[0], p[7]=p[1], etc... for (int i=0; i < n; ++i) { draw(graph(TPC(i),-2*pi,2*pi), bp+p[i], legend="$T_{"+(string)i+"}$"); } xlimits(-2*pi,2*pi, Crop); ylimits(-4,4, Crop); attach(legend(linelength=3mm),point(E),5E); shipout(bbox(Fill(lightgrey)));
graph-fig029
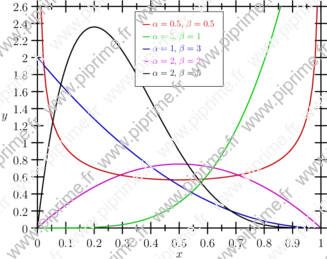
Beta distribution.
Show graph/fig0300.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Function (drawing) | #Legend | #Typedef
import graph; unitsize(10cm,3cm); typedef real realfcn(real); realfcn betaFunction(real alpha, real beta){ return new real(real x){ return gamma(alpha+beta)/(gamma(alpha)+gamma(beta))*x^(alpha-1)*(1-x)^(beta-1); }; }; real[][] ab=new real[][] {{0.5,0.5},{5,1},{1,3},{2,2},{2,5}}; pen[] p=new pen[] {0.8*red, 0.8*green, 0.8*blue, 0.8*magenta, black}; for (int i=0; i < 5; ++i) { draw(graph(betaFunction(ab[i][0],ab[i][1]),1e-5,1-1e-5), bp+p[i], legend="$\alpha="+(string)ab[i][0]+",\;\beta="+(string)ab[i][1]+"$"); } xlimits(0,1,Crop); ylimits(0,2.6,Crop); xaxis("$x$",BottomTop,linewidth(bp),Ticks); yaxis("$y$",LeftRight,linewidth(bp),Ticks(Step=0.2)); attach(scale(0.75)*legend(linelength=3mm),point(N),5S,UnFill);
graph-fig030

Other examples of interpolations can be found here.
Show graph/fig0310.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Graph.asy
Tags : #Graph | #Interpolate | #Function (drawing) | #Legend | #Typedef
import graph; unitsize(1cm); typedef real hermite(real); /** * Retourne la fonction polynôme de Hermite * passant par les points m(x_i,y_i) de nombre dérivée d_i en ce point. * Return Hermite polynomial interpolation function * passing by the points m (x_i, y_i) of derived number d_i in this point. **/ hermite hermite(pair [] m, real [] d) { return new real(real x){ int n=m.length; if (n != d.length) abort("Hermite: nombres de paramètres incorrectes."); real q,qk,s,y=0; for (int k=0; k<n ; ++k) { real q=1, qk=1, s=0; for (int j=0; j<n; ++j) { if (j!=k){ q=q*(x-m[j].x)^2; qk=qk*(m[k].x-m[j].x)^2; s=s+1/(m[k].x-m[j].x); } } y=y+q/qk*(m[k].y+(x-m[k].x)*(d[k]-2*s*m[k].y)); } return y; }; } pair[] m; real[] d; int nbpt=5; real xmin=-2pi, xmax=2pi, l=xmax-xmin, step=l/(nbpt+1); for (int i=1; i<=nbpt; ++i) { real x=xmin+i*step; m.push((x,sin(x))); draw(m[m.length-1],linewidth(2mm)); d.push(cos(x)); } xlimits(-2pi,2pi); ylimits(-2,2); xaxis("$x$",BottomTop,Ticks); yaxis("$y$",LeftRight,Ticks); draw(graph(sin,xmin,xmax),1mm+.8red,"$x\longmapsto{}\sin x$"); draw(graph(hermite(m,d),xmin,xmax),"$x\longmapsto{}H(x)$"); attach(legend(),point(10S),30S);