Category Examples 3D -- Asymptote Gallery

🔗Asymptote Gallery for Category “Examples 3D” #3

🔗graph3-fig001

A Möbius strip of half-width $w$ with midcircle of radius

$R$ and at height $z=0$ can be represented parametrically by :

$\backslash begin\{cases\}\%\; x=\backslash left(R+s\backslash times\backslash cos\; \backslash left(\backslash frac\{t\}\{2\}\backslash right)\backslash right)\backslash cos(t)\backslash \backslash \; y=\backslash left(R+s\backslash times\backslash cos\; \backslash left(\backslash frac\{t\}\{2\}\backslash right)\backslash right)\backslash sin(t)\backslash \backslash \; z=s\backslash times\backslash sin\; \backslash left(\backslash frac\{t\}\{2\}\backslash right)\; \backslash end\{cases\}$

for $s$ in $[-w\backslash ,;\backslash ,w]$ and $t$ in $[0\backslash ,;\backslash ,2\backslash pi]$. In this parametrization, the Möbius strip is therefore a cubic surface with equation

$-R2y+x2y+y3-2Rxz-2x2z-2y2z+yz2=0$

Source

Show graph3/fig0010.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Surface | #Level set (3D)

import graph3;
ngraph=200;
size(12cm,0);
currentprojection=orthographic(-4,-4,5);

real x(real t), y(real t), z(real t);

real R=2;
void xyzset(real s){
  x=new real(real t){return (R+s*cos(t/2))*cos(t);};
  y=new real(real t){return (R+s*cos(t/2))*sin(t);};
  z=new real(real t){return s*sin(t/2);};
}


int n=ngraph;
real w=1;
real s=-w, st=2w/n;
path3 p;
triple[][] ts;
for (int i=0; i <= n; ++i) {
  xyzset(s);
  p=graph(x,y,z,0,2pi);

  ts.push(new triple[] {});
  for (int j=0; j <= ngraph; ++j) {
    ts[i].push(point(p,j));
  }
  s += st;
}

pen[] pens={black, yellow, red, yellow, black};
draw(surface(ts, new bool[][]{}), lightgrey);
for (int i=0; i <= 4; ++i) {
  xyzset(-w+i*w/2);
  draw(graph(x,y,z,0,2pi), 2bp+pens[i]);
}

🔗graph3-fig002

Show graph3/fig0020.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Axis (3D)

import graph3;

size(8cm,0);
currentprojection=orthographic(1,1,1);

limits((0,-2,0),(2,2,2));

xaxis3("$x$", OutTicks());
yaxis3("$y$", OutTicks());
zaxis3("$z$", OutTicks());

🔗graph3-fig003

Show graph3/fig0030.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Axis (3D)

import graph3;

size(8cm,0,IgnoreAspect);
currentprojection=orthographic(1,1,1);

limits((0,-2,0), (2,2,2));

axes3("$x$","$y$","$z$",Arrow3);

🔗graph3-fig004

Show graph3/fig0040.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Axis (3D)

import graph3;

size(8cm,0);
currentprojection=orthographic(1,1,1);

defaultpen(overwrite(SuppressQuiet));

limits((0,-2,0),(2,2,2));

xaxis3("$x$", InTicks(XY()*Label));
yaxis3("$y$", InTicks(XY()*Label));
zaxis3("$z$", OutTicks, p=red, arrow=Arrow3);

🔗graph3-fig005

Show graph3/fig0050.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Axis (3D)

import graph3;

size(6cm,0);
currentprojection=orthographic(1,1,1);

limits((-2,-2,0),(0,2,2));

xaxis3(Label("$x$",MidPoint), OutTicks());
yaxis3("$y$", InTicks());
zaxis3("$z$",XYEquals(-2,0), OutTicks());

🔗graph3-fig006

Show graph3/fig0060.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Axis (3D)

import graph3;
usepackage("icomma");

size(8cm,0);
currentprojection=orthographic(1.5,1,1);

limits((-2,-1,-.5), (0,1,1.5));

xaxis3("$x$",
       Bounds(Both,Value),
       OutTicks(endlabel=false));

yaxis3("$y$",
       Bounds(Both,Value),
       OutTicks(Step=.5,step=.25));

zaxis3("$z$", XYEquals(-2,0), InOutTicks(Label(align=Y-X)));

dot(Label("",align=Z), (-1,0,0), red);

🔗graph3-fig007

Show graph3/fig0070.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Axis (3D) | #Triple

import graph3;

size(8cm,0);
currentprojection=orthographic(1,1,0.5);
limits((-2,-2,0),(0,2,2));

xaxis3(Label("$x$",align=Z),
       Bounds(Min,Min),
       OutTicks(endlabel=false,Step=1,step=0.5));

yaxis3("$y$", Bounds(),
       OutTicks(pTick=0.8*red, ptick=lightgrey));

zaxis3("$z$", Bounds(),
       OutTicks, p=red, arrow=Arrow3);

dot(Label("",align=Z), (-1,0,0), red);

🔗graph3-fig008

Show graph3/fig0080.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Surface | #Level set (3D) | #Contour | #Function (implicit)

// Adapted from the documentation of Asymptote.
import graph3;
import contour;
texpreamble("\usepackage{icomma}");

size3(12cm, 12cm, 8cm, IgnoreAspect);

real sinc(pair z) {
  real r=2pi*abs(z);
  return r != 0 ? sin(r)/r : 1;
}

limits((-2, -2, -0.2), (2, 2, 1.2));
currentprojection=orthographic(1, -2, 0.5);

xaxis3(rotate(90, X)*"$x$",
       Bounds(Min, Min),
       OutTicks(rotate(90, X)*Label, endlabel=false));

yaxis3("$y$", Bounds(Max, Min), InTicks(Label));
zaxis3("$z$", Bounds(Min, Min), OutTicks());

draw(lift(sinc, contour(sinc, (-2, -2), (2, 2), new real[] {0})), bp+0.8*red);
draw(surface(sinc, (-2, -2), (2, 2), nx=100, Spline), lightgray);

draw(scale3(2*sqrt(2))*unitdisk, paleyellow+opacity(0.25), nolight);
draw(scale3(2*sqrt(2))*unitcircle3, 0.8*red);

🔗graph3-fig009

Show graph3/fig0090.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Surface | #Level set (3D) | #Contour | #Function (implicit) | #Palette

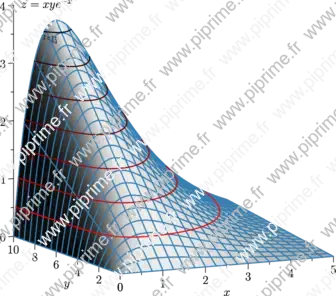
size(12cm,0,false);
import graph3;
import contour;
import palette;

texpreamble("\usepackage{icomma}");

real f(pair z) {return z.x*z.y*exp(-z.x);}

currentprojection=orthographic(-2.5,-5,1);

draw(surface(f,(0,0),(5,10),20,Spline),palegray,bp+rgb(0.2,0.5,0.7));

scale(true);

xaxis3(Label("$x$",MidPoint),OutTicks());
yaxis3(Label("$y$",MidPoint),OutTicks(Step=2));
zaxis3(Label("$z=xye^{-x}$",Relative(1),align=2E),Bounds(Min,Max),OutTicks);

real[] datumz={0.5,1,1.5,2,2.5,3,3.5};

Label[] L=sequence(new Label(int i) {
    return YZ()*(Label(format("$z=%g$",datumz[i]),
                       align=2currentprojection.vector()-1.5Z,Relative(1)));
  },datumz.length);

pen fontsize=bp+fontsize(10);
draw(L,lift(f,contour(f,(0,0),(5,10),datumz)),
     palette(datumz,Gradient(fontsize+red,fontsize+black)));

🔗graph3-fig010

Show graph3/fig0100.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph | #Contour | #Function (implicit) | #Palette | #Axis | #Array

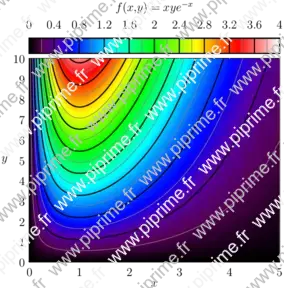
// From documentation of Asymptote
import graph;
import palette;
import contour;
texpreamble("\usepackage{icomma}");

size(10cm,10cm,IgnoreAspect);

pair a=(0,0);
pair b=(5,10);

real fz(pair z) {
  return z.x*z.y*exp(-z.x);
}
real f(real x, real y) {return fz((x,y));}

int N=200;
int Divs=10;
int divs=2;

defaultpen(1bp);
pen Tickpen=black;
pen tickpen=gray+0.5*linewidth(currentpen);
pen[] Palette=BWRainbow();

scale(false);

bounds range=image(f,Automatic,a,b,N,Palette);

xaxis("$x$",BottomTop,LeftTicks(pTick=grey, ptick=invisible, extend=true));
yaxis("$y$",LeftRight,RightTicks(pTick=grey, ptick=invisible, extend=true));

// Major contours
real[] Cvals;
Cvals=sequence(11)/10 * (range.max-range.min) + range.min;
draw(contour(f,a,b,Cvals,N,operator ..),Tickpen);

// Minor contours
real[] cvals;
real[] sumarr=sequence(1,divs-1)/divs * (range.max-range.min)/Divs;
for (int ival=0; ival < Cvals.length-1; ++ival)
    cvals.append(Cvals[ival]+sumarr);
draw(contour(f,a,b,cvals,N,operator ..),tickpen);

palette("$f(x,y)=xye^{-x}$",range,point(NW)+(0,1),point(NE)+(0,0.25),Top,Palette,
        PaletteTicks(N=Divs,n=divs,Tickpen,tickpen));

🔗graph3-fig011

Show graph3/fig0110.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Surface | #Level set (3D) | #Contour | #Function (implicit) | #Palette | #Projection (3D) | #Axis (3D) | #Label (3D) | #Shading (3D) | #Shading

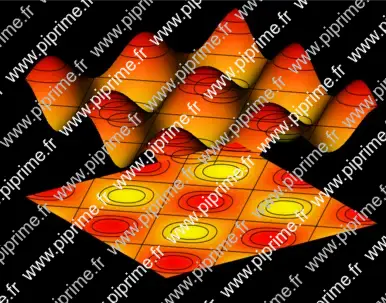
import graph3;
import palette;
import contour;
size(14cm,0);
currentprojection=orthographic(-1,-1.5,0.75);
currentlight=(-1,0,5);

real a=1, b=1;
real f(pair z) { return a*(6+sin(z.x/b)+sin(z.y/b));}
real g(pair z){return f(z)-6a;}

// The axes
limits((0,0,4a),(14,14,8a));
xaxis3(Label("$x$",MidPoint),OutTicks());
yaxis3(Label("$y$",MidPoint),OutTicks(Step=2));
ticklabel relativelabel()
{
  return new string(real x) {return (string)(x-6a);};
}
zaxis3(Label("$z$",Relative(1),align=2E),Bounds(Min,Max),OutTicks(relativelabel()));

// The surface
surface s=surface(f,(0,0),(14,14),100,Spline);

pen[] pens=mean(palette(s.map(zpart),Gradient(yellow,red)));

// Draw the surface
draw(s,pens);
// Project the surface onto the XY plane.
draw(planeproject(unitsquare3)*s,pens,nolight);

// Draw contour for "datumz"
real[] datumz={-1.5, -1, 0, 1, 1.5};
guide[][] pl=contour(g,(0,0),(14,14),datumz);
for (int i=0; i < pl.length; ++i)
  for (int j=0; j < pl[i].length; ++j)
    draw(path3(pl[i][j]));

// Draw the contours on the surface
draw(lift(f,pl));

if(!is3D())
  shipout(bbox(3mm,Fill(black)));

🔗graph3-fig012

Show graph3/fig0120.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Projection (3D) | #Shading (3D)

import graph3;
import palette;

real sinc(real x){return x != 0 ? sin(x)/x : 1;}

real f(pair z){
  real value = (sinc(pi*z.x)*sinc(pi*z.y))**2;
  return value^0.25;
}

currentprojection=orthographic(0,0,1);

size(10cm,0);

surface s=surface(f,(-5,-5),(5,5),100,Spline);
s.colors(palette(s.map(zpart),Gradient((int)2^11 ... new pen[]{black,white})));

draw(planeproject(unitsquare3)*s,nolight);

🔗graph3-fig013

From TeXgraph exemples.

Show graph3/fig0130.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D)

settings.render=0;
import graph3;
import palette;
size(10cm,0);
currentprojection=orthographic(2,-2,2.5);

real f(pair z) {
  real u=z.x, v=z.y;
  return (u/2+v)/(2+cos(u/2)*sin(v));
}

surface s=surface(f,(0,0),(14,14),150,Spline);
draw(s,mean(palette(s.map(zpart),Gradient(yellow,red))));

if(!is3D())
  shipout(bbox(3mm,Fill(black)));

🔗graph3-fig014

From TeXgraph exemples.

Show graph3/fig0140.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D)

settings.render=0;
import graph3;
import palette;
size(15cm,0);
currentprojection=orthographic(2,-2,2.5);

real f(pair z) {
  real u=z.x, v=z.y;
  return (u/2+v)/(2+cos(u/2)*sin(v));
}

surface s=surface(f,(0,0),(14,14),50,Spline);
s.colors(palette(s.map(zpart),Gradient(yellow,red)));

draw(s);

if(!is3D())
  shipout(bbox(3mm,Fill(black)));

🔗graph3-fig015

Show graph3/fig0150.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D) | #Array | #Spherical harmonics

settings.render=0;
import graph3;
size(15cm);

currentprojection=orthographic(4,2,4);

real r(real Theta, real Phi){return 1+0.5*(sin(2*Theta)*sin(2*Phi))^2;}
triple f(pair z) {return r(z.x,z.y)*expi(z.x,z.y);}

pen[] pens(triple[] z)
{
  return sequence(new pen(int i) {
      real a=abs(z[i]);
      return a < 1+1e-3 ? black : interp(blue, red, 2*(a-1));
    },z.length);
}

surface s=surface(f,(0,0),(pi,2pi),100,Spline);
// Interpolate the corners, and coloring each patch with one color
// produce some artefacts
draw(s,pens(s.cornermean()));

if(!is3D())
  shipout(bbox(3mm,Fill(black)));

🔗graph3-fig016

Show graph3/fig0160.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D) | #Array | #Spherical harmonics

settings.render=0;
import graph3;
size(15cm);

currentprojection=orthographic(4,2,4);

real r(real Theta, real Phi){return 1+0.5*(sin(2*Theta)*sin(2*Phi))^2;}
triple f(pair z) {return r(z.x,z.y)*expi(z.x,z.y);}

pen[][] pens(triple[][] z)
{
  pen[][] p=new pen[z.length][];
  for(int i=0; i < z.length; ++i) {
    triple[] zi=z[i];
    p[i]=sequence(new pen(int j) {
	real a=abs(zi[j]);
	return a < 1+1e-3 ? black : interp(blue, red, 2*(a-1));},
      zi.length);
  }
  return p;
}

surface s=surface(f,(0,0),(pi,2pi),100,Spline);
// Here we interpolate the pens, this looks smoother, with fewer artifacts
draw(s,mean(pens(s.corners())));

if(!is3D())
  shipout(bbox(3mm,Fill(black)));

🔗graph3-fig017

Show graph3/fig0170.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D) | #Array | #Spherical harmonics

import graph3;
size(16cm, 0);

currentprojection=orthographic(4, 2, 4);

real r(real Theta, real Phi){return 1+0.5*(sin(2*Theta)*sin(2*Phi))^2;}
triple f(pair z) {return r(z.x, z.y)*expi(z.x, z.y);}

pen[][] pens(triple[][] z)
{
  pen[][] p=new pen[z.length][];
  for(int i=0; i < z.length; ++i) {
    triple[] zi=z[i];
    p[i]=sequence(new pen(int j) {
    real a=abs(zi[j]);

    return a < 1+1e-3 ? black : interp(blue, red, 2*(a-1));}, zi.length);
  }

  return p;
}

surface s=surface(f, (0, 0), (pi, 2pi), 100, Spline);
// Here we determine the colors of vertexes (vertex shading).
// Since the PRC output format does not support vertex shading of Bezier surfaces, PRC patches
// are shaded with the mean of the four vertex colors.
s.colors(pens(s.corners()));
draw(s);

if(!is3D())
  shipout(bbox(1mm, Fill(black)));

🔗graph3-fig018

The spherical harmonics $Y\_l^m(\backslash theta,\backslash varphi)$ are the angular portion of the solution to Laplace's equation in spherical coordinates where azimuthal symmetry is not present.

The spherical harmonics are defined by:

$Y\_l^m(\backslash theta,\backslash varphi)=\backslash sqrt\{\backslash frac\{2l+1\}\{4\backslash pi\}\backslash frac\{(l-m)!\}\{(l+m)!\}\}P\_\{l\}^\{m\}(\backslash cos\backslash theta)e^\{im\backslash varphi\}$

where $m=-l,\backslash ,-(l-1),\backslash ,\backslash ldots,\backslash ,0,\backslash ,\backslash ldots,\backslash ,l-1,\backslash ,l$ and $P\_l^m$ is the Legendre polynomial.

Source

Show graph3/fig0180.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D) | #Spherical harmonics

import palette;
import math;
import graph3;

typedef real fct(real);
typedef pair zfct2(real,real);
typedef real fct2(real,real);

real binomial(real n, real k)
{
  return gamma(n+1)/(gamma(n-k+1)*gamma(k+1));
}

real factorial(real n) {
  return gamma(n+1);
}

real[] pdiff(real[] p)
{ // p(x)=p[0]+p[1]x+...p[n]x^n
  // retourne la dérivée de p
  real[] dif;
  for (int i : p.keys) {
    if(i != 0) dif.push(i*p[i]);
  }
  return dif;
}

real[] pdiff(real[] p, int n)
{ // p(x)=p[0]+p[1]x+...p[n]x^n
  // dérivée n-ième de p
  real[] dif={0};
  if(n >= p.length) return dif;
  dif=p;
  for (int i=0; i < n; ++i)
    dif=pdiff(dif);
  return dif;
}

fct operator *(real y, fct f)
{
  return new real(real x){return y*f(x);};
}

zfct2 operator +(zfct2 f, zfct2 g)
{// Défini f+g
  return new pair(real t, real p){return f(t,p)+g(t,p);};
}

zfct2 operator -(zfct2 f, zfct2 g)
{// Défini f-g
  return new pair(real t, real p){return f(t,p)-g(t,p);};
}

zfct2 operator /(zfct2 f, real x)
{// Défini f/x
  return new pair(real t, real p){return f(t,p)/x;};
}

zfct2 operator *(real x,zfct2 f)
{// Défini x*f
  return new pair(real t, real p){return x*f(t,p);};
}

fct fct(real[] p)
{ // convertit le tableau des coefs du poly p en fonction polynôme
  return new real(real x){
    real y=0;
    for (int i : p.keys) {
      y += p[i]*x^i;
    }
    return y;
  };
}

real C(int l, int m)
{
  if(m < 0) return 1/C(l,-m);
  real OC=1;
  int d=l-m, s=l+m;
  for (int i=d+1; i <=s ; ++i) OC *= i;
  return 1/OC;
}

int csphase=-1;
fct P(int l, int m)
{ // Polynôme de Legendre associé
  // http://mathworld.wolfram.com/LegendrePolynomial.html
  if(m < 0) return (-1)^(-m)*C(l,-m)*P(l,-m);
  real[] xl2;
  for (int k=0; k <= l; ++k) {
    xl2.push((-1)^(l-k)*binomial(l,k));
    if(k != l) xl2.push(0);
  }
  fct dxl2=fct(pdiff(xl2,l+m));
  return new real(real x){
    return (csphase)^m/(2^l*factorial(l))*(1-x^2)^(m/2)*dxl2(x);
  };
}

zfct2 Y(int l, int m)
{// http://fr.wikipedia.org/wiki/Harmonique_sph%C3%A9rique#Expression_des_harmoniques_sph.C3.A9riques_normalis.C3.A9es
  return new pair(real theta, real phi) {
    return sqrt((2*l+1)*C(l,m)/(4*pi))*P(l,m)(cos(theta))*expi(m*phi);
  };
}

real xyabs(triple z){return abs(xypart(z));}

size(16cm);
currentprojection=orthographic(0,1,1);

zfct2 Ylm;

triple F(pair z)
{
  //   real r=0.75+dot(0.25*I,Ylm(z.x,z.y));
  //   return r*expi(z.x,z.y);
  real r=abs(Ylm(z.x,z.y))^2;
  return r*expi(z.x,z.y);
}

int nb=4;
for (int l=0; l < nb; ++l) {
  for (int m=0; m <= l; ++m) {
    Ylm=Y(l,m);

    surface s=surface(F,(0,0),(pi,2pi),60);
    s.colors(palette(s.map(xyabs),Rainbow()));

    triple v=(-m,0,-l);
    draw(shift(v)*s);
    label("$Y_"+ string(l) + "^" + string(m) + "$:",shift(X/3)*v);
  }
}

🔗grid3-fig001

Show grid3/fig0100.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Grid3.asy
Tags : #Graph (3D) | #Grid (3D) | #Axis (3D)

import grid3;

size(10cm,0,IgnoreAspect);
currentprojection=orthographic(0.25, 1, 0.25);

limits((-2,-2,0), (0,2,2));

grid3(
      pic=currentpicture,            // picture (default=currentpicture)

      gridroutine=XYZgrid(           // gridtype3droutine or gridtype3droutine [] (alias gridtype3droutines)
                          //                         or gridtype3droutines []:
                          //                         The routine(s) to draw the grid(s);
                          //                         the values can be as follows:
                          //                            * XYgrid : draw grid from X in direction of Y
                          //                            * YXgrid : draw grid from Y in direction of X
                          //                                etc...
                          //                            * An array of previous values XYgrid, YXgrid, ...
                          //                            * XYXgrid : draw XYgrid and YXgrid grids
                          //                            * YXYgrid : draw XYgrid and YXgrid grids
                          //                            * ZXZgrid : draw ZXgrid and XZgrid grids
                          //                            * YX_YZgrid : draw YXgrid and YZgrid grids
                          //                            * XY_XZgrid : draw XYgrid and XZgrid grids
                          //                            * YX_YZgrid : draw YXgrid and YZgrid grids
                          //                            * An array of previous values XYXgrid, YZYgrid, ...
                          //                            * XYZgrid : draw XYXgrid, ZYZgrid and XZXgrid grids.
                          pos=Relative(0)), // position (default=Relative(0)) :
      //                          this is the position of the grid relatively to
      //                          the perpendicular axe of the grid.
      //                          If 'pos' is a the real, 'pos' is a coordinate relativly to this axe.
      //                          Alias 'top=Relative(1)', 'middle=Relative(0.5)'
      //                          and 'bottom=Relative(0)' can be used as value.

      // Following arguments are similar as the function 'Ticks'.
      N=0,                // int (default=0)
      n=0,                // int (default=0)
      Step=0,             // real (default=0)
      step=0,             // real (default=0)
      begin=true,         // bool (default=true)
      end=true,           // bool (default=true)
      pGrid=grey,         // pen (default=grey)
      pgrid=lightgrey,    // pen (default=lightgrey)
      above=false         // bool (default=false)
      );

xaxis3(Label("$x$",position=EndPoint,align=S), Bounds(Min,Min), OutTicks());
yaxis3(Label("$y$",position=EndPoint,align=S), Bounds(Min,Min), OutTicks());
zaxis3(Label("$z$",position=EndPoint,align=(0,0.5)+W), Bounds(Min,Min), OutTicks(beginlabel=false));

🔗grid3-fig002

Show grid3/fig0200.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Grid3.asy
Tags : #Graph (3D) | #Grid (3D) | #Axis (3D)

import grid3;

size(10cm,0,IgnoreAspect);
currentprojection=orthographic(0.25, 1, 0.25);

limits((-2,-2,0), (0,2,2));

scale(Linear, Linear, Log(automax=false));
grid3(XZXgrid);
grid3(XYXgrid);
xaxis3(Label("$x$",position=EndPoint,align=S), Bounds(Min,Min), OutTicks());
yaxis3(Label("$y$",position=EndPoint,align=S), Bounds(Min,Min), OutTicks());
zaxis3(Label("$z$",position=EndPoint,align=(0,0.5)+W), Bounds(Min,Min), OutTicks(beginlabel=false));

🔗grid3-fig003

Show grid3/fig0300.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Grid3.asy
Tags : #Graph (3D) | #Grid (3D) | #Axis (3D)

import grid3;

size(10cm,0,IgnoreAspect);
currentprojection=orthographic(0.25, 1, 0.25);
limits((-2,-2,0), (0,2,2));

grid3(new grid3routines [] {XYXgrid(Relative(1)), XZXgrid(0)});

xaxis3(Label("$x$",position=EndPoint,align=S), Bounds(Min,Min), OutTicks());
yaxis3(Label("$y$",position=EndPoint,align=S), Bounds(Min,Min), OutTicks());
zaxis3(Label("$z$",position=EndPoint,align=(0,.5)+W), Bounds(Min,Min), OutTicks(beginlabel=false));

🔗grid3-fig004

Show grid3/fig0400.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Grid3.asy
Tags : #Graph (3D) | #Grid (3D) | #Axis (3D)

import grid3;

size(10cm,0,IgnoreAspect);
currentprojection=orthographic(0.25, 1, 0.25);
limits((-2,-2,0),(0,2,2));

grid3(new grid3routines [] {XYXgrid(-0.5), XYXgrid(1.5)},
      pGrid=new pen[] {red, blue},
      pgrid=new pen[] {0.5red, 0.5blue});
xaxis3(Label("$x$",position=EndPoint,align=Z), YZEquals(-2,0), OutTicks());
yaxis3(Label("$y$",position=EndPoint,align=Z), XZEquals(-2,0), OutTicks());
zaxis3(Label("$z$",position=EndPoint,align=X), XYEquals(-2,-2), OutTicks(Label("",align=-X-Y)));

🔗grid3-fig005

Show grid3/fig0500.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Grid3.asy
Tags : #Graph (3D) | #Grid (3D) | #Axis (3D)

import grid3;

size(10cm,0,IgnoreAspect);
currentprojection=orthographic(0.25,1,0.25);
limits((-2,-2,0),(0,2,2));

real Step=0.5, step=0.25;
xaxis3(Label("$x$",position=EndPoint,align=Z), YZEquals(-2,0),
       InOutTicks(Label(align=0.5*(Z-Y)),
                  Step=Step, step=step,
                  gridroutine=XYgrid,
                  pGrid=red, pgrid=0.5red));

yaxis3(Label("$y$",position=EndPoint,align=Z), XZEquals(-2,0),
       InOutTicks(Label(align=-0.5*(X-Z)), Step=Step, step=step,
                  gridroutine=YXgrid,
                  pGrid=red, pgrid=0.5red));

zaxis3("$z$", XYEquals(-1,0), OutTicks(Label(align=-0.5*(X+Y))));

🔗grid3-fig006

Show grid3/fig0600.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Grid3.asy
Tags : #Graph (3D) | #Grid (3D) | #Axis (3D)

import grid3;

size(10cm,0,IgnoreAspect);
currentprojection=orthographic(0.25,1,0.25);
limits((-2,-2,0),(0,2,2));

xaxis3(Label("$x$",position=EndPoint,align=Z), YZEquals(-2,0),
       OutTicks(Label(align=0.5*(Z-Y)),Step=0.5, gridroutine=XYgrid));

yaxis3(Label("$y$",position=EndPoint,align=-X), XZEquals(-2,0),
       InOutTicks(Label(align=0.5*(Z-X)),N=8,n=2, gridroutine=YX_YZgrid));

zaxis3("$z$", OutTicks(ZYgrid));

🔗solids-fig001

Show solids/fig0010.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Light (3D) | #Draw (3D) | #Surface | #Sphere | #Revolution | #Projection (3D)

import solids;
import three;
currentprojection=orthographic(1,2,2);

size(6cm,0);

material m = material(
  diffusepen=yellow,
  emissivepen=black,
  specularpen=orange,
  shininess=0.25,
  metallic=0.5,
  fresnel0=0.07
);

draw(surface(sphere(1)), m);

🔗solids-fig002

Show solids/fig0020.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Light (3D) | #Draw (3D) | #Surface | #Sphere | #Revolution | #Projection (3D)

import solids;
currentlight=light(paleyellow, specularfactor=3, (2,4,6));

size(6cm,0);
draw(sphere(1,n=4*nslice), linewidth(bp), m=10);
draw(surface(sphere(1,n=4*nslice)), orange);

🔗solids-fig003

Show solids/fig0030.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Revolution | #Projection (3D) | #Draw (3D) | #Surface | #Sphere | #Wire frame | #Line type

// Author: John Bowman.
size(6cm, 0);
import solids;
currentprojection=orthographic(0, 10, 5);

nslice=4*nslice;

revolution r=sphere(O, 1);
draw(surface(r), lightgrey+opacity(0.75));

skeleton s;
r.transverse(s, reltime(r.g, 0.6), currentprojection);
r.transverse(s, reltime(r.g, 0.5), currentprojection);
draw(s.transverse.back, linetype("8 8", 8));
draw(s.transverse.front);

r.longitudinal(s, currentprojection);
draw(s.longitudinal.front);
draw(s.longitudinal.back, linetype("8 8", 8));

🔗solids-fig004

Show solids/fig0040.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Transform (3D) | #Revolution | #Surface | #Sphere | #Projection (3D)

import solids;
size(6cm,0);

currentprojection=orthographic(100,150,30);

real r=1;

skeleton s;
revolution sph=sphere(O,r);
draw(surface(sph), palegray);

path3 cle=rotate(90,X)*scale3(r)*unitcircle3;

triple cam=unit(currentprojection.camera);
real a=degrees(xypart(cam),false)-90;
real b=-sgn(cam.z)*aCos(sqrt(cam.x^2+cam.y^2)/abs(cam));
cle=rotate(b,cross(Z,cam))*rotate(a,Z)*cle;
draw(cle,4pt+red);

🔗solids-fig005

Show solids/fig0050.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Projection (3D) | #Solid | #Transform (3D) | #Revolution | #Surface | #Sphere | #Light (3D)

import solids;
size(6cm,0);
currentlight=light(diffuse=yellow, specular=blue, specularfactor=5, (5,-5,10));
// currentprojection=orthographic(100,100,30);
real r=2;

skeleton s;
revolution sph=sphere(O,r);
draw(surface(sph),red);

triple cam=unit(currentprojection.camera);
revolution cle=revolution(O,r*(rotate(90,Z)*cam),cam);
draw(cle, 8pt+black);

🔗solids-fig006

Show solids/fig0060.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Transform (3D) | #Sphere | #Projection (3D) | #

// Author: John Bowman
import three;
size(6cm,0);
currentprojection=perspective(10,100,50);
real a=2.5;

draw(scale3(a)*unitsphere,lightyellow);
draw(align(unit(currentprojection.vector()))*scale3(a)*unitcircle3,2bp+red);

🔗solids-fig007

Show solids/fig0070.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Surface | #Sphere | #Draw (3D)

import solids;
size(6cm,0);
currentprojection=orthographic(1,2,2);

surface s=surface(sphere(1,n=10));

material m = material(
  diffusepen = 0.8*red,
  emissivepen= yellow,
  specularpen= red
);

material[] p={m, red, 0.8*(red+blue) , green, 0.8*blue};
p.cyclic=true;

draw(s,p);

🔗solids-fig008

Show solids/fig0080.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Plane | #Shading (3D) | #Transform (3D) | #Projection (3D) | #Surface | #Palette

import solids;
import palette;
size(14cm,0);
currentlight=light(
  gray(0.4),
  specularfactor=3,
  (-0.5,-0.25,0.45),
  (0.5,-0.5,0.5),(0.5,0.5,0.75)
);

nslice=4*nslice;
surface s=surface(sphere(O,1));
draw(s,lightgrey);

path3 pl=plane((1,0,0),(0,1,0),(0,0,-1));
surface pls=shift(3,3,-1e-3)*scale(-6,-6,1)*surface(pl);
draw(pls,0.7*red);

real dist(triple z){return abs(z-Z);}

surface shade;
for (int i=0; i < currentlight.position.length; ++i) {
  shade=planeproject(pl,currentlight.position[i])*s;
  draw(shade,mean(palette((shade.map(dist)),
                          Gradient(black,gray(0.6)))),
       nolight);
}

🔗solids-fig009

Show solids/fig0090.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Arc (3D) | #Markers | #Revolution | #Surface | #Sphere

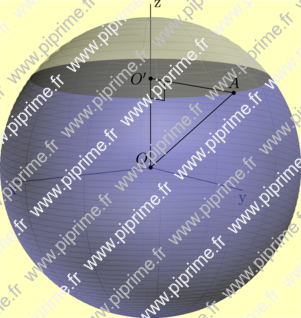
size(8cm, 0);
import solids;
import graph3;

//Draw 3D right angle (MA, MB)
void drawrightangle(picture pic=currentpicture,
                    triple M, triple A, triple B,
                    real radius=0,
                    pen p=currentpen,
                    pen fillpen=nullpen,
                    projection P=currentprojection)
{
  p=linejoin(0)+linecap(0)+p;
  if (radius==0) radius=arrowfactor*sqrt(2);
  transform3 T=shift(-M);
  triple OA=radius/sqrt(2)*unit(T*A),
    OB=radius/sqrt(2)*unit(T*B),
    OC=OA+OB;
  path3 tp=OA--OC--OB;
  picture tpic;
  draw(tpic, tp, p=p);
  if (fillpen!=nullpen) draw(tpic, surface(O--tp--cycle), fillpen);
  add(pic, tpic, M);
}

currentprojection=orthographic(10, 15, 3);

real r=10, h=6; // r=sphere radius; h=altitude section
triple Op=(0, 0, h);

limits((0, 0, 0), 1.1*(r, r, r));
axes3("x", "y", "z");

real rs=sqrt(r^2-h^2); // section radius
real ch=180*acos(h/r)/pi;
path3 arcD=Arc(O, r, 180, 0, ch, 0, Y, 50);

revolution sphereD=revolution(O, arcD, Z);
draw(surface(sphereD), opacity(0.5)+lightblue);
draw(shift(0, 0, h)*scale3(rs)*surface(unitcircle3), opacity(0.5));

path3 arcU=Arc(O, r, ch, 0, 0, 0, Y, 10);
revolution sphereU=revolution(O, arcU, Z);
draw(surface(sphereU), opacity(0.33)+lightgrey);

// right triangle OO'A
triple A=rotate(100, Z)*(rs, 0, h);
dot("$O$", O, NW);
dot("$O'$", Op, W);
dot("$A$", A, N);
draw(A--O--Op--A);
drawrightangle(Op, O, A);

if(!is3D())
  shipout(format="pdf", bbox(Fill(paleyellow)));

🔗solids-fig010

Show solids/fig0100.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Revolution | #Wire frame | #Surface

unitsize(1cm);
import solids;

currentprojection=orthographic(0, 100, 25);

real r=4, h=7;
triple O=(0, 0, 0);
triple Oprime=(0, 0, 3);
triple pS=(0, 0, h);
triple pA=(r*sqrt(2)/2, r*sqrt(2)/2, 0);
revolution rC=cone(O, r, h, axis=Z, n=1);

draw(surface(rC), blue+opacity(0.5));

skeleton s;
real tOprime=abs(Oprime)/h;
rC.transverse(s, reltime(rC.g, tOprime), currentprojection);
triple pAprime=relpoint(pA--pS, tOprime);
draw(s.transverse.back, dashed);
draw(s.transverse.front);

label("$S$", pS, N);
dot(Label("$O$", align=SE), O);
dot(Label("$O'$", align=SE), Oprime);
dot(Label("$A$", align=Z), pA);
dot(Label("$A'$", align=Z), pAprime);

draw(pS--O^^O--pA^^Oprime--pAprime, dashed);

🔗solids-fig011

Show solids/fig0110.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Revolution | #Wire frame | #Sphere

import solids;
unitsize(4cm);

currentprojection=orthographic(2,2,1);

draw(cylinder(c=(0,0,-1.5),r=1,h=3), m=3);
draw(sphere(r=1), m=2, frontpen=defaultbackpen);

🔗solids-fig012

Show solids/fig0120.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Intersection | #Revolution | #Wire frame | #Markers

import solids;

size(10cm, 0);
currentprojection=orthographic(-50, 100, 40);

//Draw right angle (MA, MB) in 3D
void drawrightangle(picture pic=currentpicture,
                    triple M, triple A, triple B,
                    real radius=0,
                    pen p=currentpen,
                    pen fillpen=nullpen,
                    projection P=currentprojection)
{
  p=linejoin(0)+linecap(0)+p;
  if (radius==0) radius=arrowfactor*sqrt(2);
  transform3 T=shift(-M);
  triple OA=radius/sqrt(2)*unit(T*A),
    OB=radius/sqrt(2)*unit(T*B),
    OC=OA+OB;
  path3 _p=OA--OC--OB;
  picture pic_;
    draw(pic_, _p, p=p);
    if (fillpen!=nullpen) draw(pic_, surface(O--_p--cycle), fillpen);
  add(pic, pic_, M);
}

// *...............Construction starts here................*

real r=1, h=.75;
real gle=60;
real gleA=20;
transform3 tR=rotate(gle, Z);
transform3 tT=shift((0, 0, -h));

triple H=(0, 0, h),//the label is O in the picture.
  A=rotate(gleA, Z)*(0, r, h),
  F=tR*A,
  B=tR*F,
  D=tT*A,
  C=tT*B,
  Ei=intersectionpoint(H--F, A--B);

revolution r=cylinder(O, r, h, Z);
// draw(surface(r));
draw(r);

draw(O--H, dashed);
draw(O--D--C--cycle^^O--H^^B--C, dashed);

drawrightangle(Ei, H, B, fillpen=black);

dot(Label("$O'$", align=invert(NE+E, O)), O);
// layer();
draw(surface(A--B--C--D--cycle), lightgrey+opacity(.5));

dot(Label("$A$", align=NW), A);
dot(Label("$B$", align=N), B);
dot(Label("$C$", align=S), C);
dot(Label("$D$", align=NW), D);
dot(Label("$E$", align=S), Ei);
dot(Label("$F$", align=S), F);
dot(Label("$O$", align=N), H);

draw(H--B--F--A--cycle^^H--F^^A--B^^A--D);

🔗solids-fig013

Show solids/fig0130.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Label (3D) | #Transform (3D) | #Projection (3D) | #Revolution

import solids;
size(8cm,0);
currentprojection=orthographic((2, 1, 2));

revolution r=cylinder((0, 0, 0), 1, -10, X);

draw(r);
draw("$x$",O--X,Arrow3);
draw("$y$",O--Y,Arrow3);
draw("$z$",O--Z,Arrow3);

label(XY()*(scale(2.5)*"This is not a cylinder"), (-5,0,1), align=Z);

🔗solids-fig014

Author : Jens Schwaiger.
With its pleasant authorization.

Show solids/fig0140.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Polyhedron | #Surface

size(10cm,0);
import bsp;

currentprojection=perspective(10,3,-2);
guide achteck=polygon(8);
real lge=length(point(achteck,1)-point(achteck,0));
int n=8;
face[] faces;
guide3[] sq;
guide3[] tr;
triple a,b,c,d;

a=(point(achteck,0).x,point(achteck,0).y,-lge/2);
b=(point(achteck,1).x,point(achteck,1).y,-lge/2);
c=(point(achteck,1).x,point(achteck,1).y,lge/2);
d=(point(achteck,0).x,point(achteck,0).y,lge/2);

sq[0]=a--b--c--d--cycle;
for(int i=1;i<n;i=i+1) sq[i]=rotate(45*i,Z)*sq[0];
for(int i=0;i<3;i=i+1) sq[n+i]=rotate(90,Y)*sq[i];
for(int i=4;i<7;i=i+1) sq[n-1+i]=rotate(90,Y)*sq[i];
for(int i=2;i<3;i=i+1) sq[12+i]=rotate(90,X)*sq[i];
sq[14]=rotate(90,X)*sq[2];
sq[15]=rotate(90,X)*sq[4];
sq[16]=rotate(90,X)*sq[6];
sq[17]=rotate(90,X)*sq[0];

tr[0]=point(sq[2],3)--point(sq[2],2)--point(sq[14],1)--cycle;
for(int i=1;i<4;i=i+1) tr[i]=rotate(90*i,Z)*tr[0];
tr[4]=reverse(point(sq[2],0)--point(sq[2],1)--point(sq[9],2)--cycle);
for(int i=5;i<8;i=i+1) tr[i]=rotate(90*(i-4),Z)*tr[4];

real hgtsq=3;
triple[][][] pyrsq=new triple[18][4][3];
path3[] pyrsqfc=new path3[4*18];
int nofface=0;
for(int i=0;i<18;i=i+1){
  triple cog=0.5(point(sq[i],0)+point(sq[i],2));
  triple sp=cog+
    hgtsq*unit(cross(point(sq[i],1)-point(sq[i],0),point(sq[i],3)-point(sq[i],0)));
  for(int j=0;j<3;j=j+1){
    pyrsq[i][j][0]=point(sq[i],j);
    pyrsq[i][j][1]=point(sq[i],j+1);
    pyrsq[i][j][2]=sp;
    pyrsqfc[nofface]=pyrsq[i][j][0]--pyrsq[i][j][1]--pyrsq[i][j][2]--cycle;
    nofface=nofface+1;
  }
  pyrsq[i][3][0]=point(sq[i],3);
  pyrsq[i][3][1]=point(sq[i],0);
  pyrsq[i][3][2]=sp;
  pyrsqfc[nofface]=pyrsq[i][3][0]--pyrsq[i][3][1]--pyrsq[i][3][2]--cycle;
  nofface=nofface+1;
 }

for(int i=0;i<18*4;i=i+1) faces.push(pyrsqfc[i]);
for(int i=0;i<18*4;i=i+1) filldraw(faces[i],project(pyrsqfc[i]),yellow,black+2.5bp);

path3[] pyrtrfc=new path3[3*8];
real hgttr=2;
int nuoftr=0;

for(int i=0;i<8;i=i+1){
  triple cog=(1/3)*(point(tr[i],0)+point(tr[i],1)+point(tr[i],2));
  triple sp=cog+hgttr*unit(cross(point(tr[i],1)-point(tr[i],0),point(tr[i],2)-point(tr[i],0)));
  pyrtrfc[nuoftr]=point(tr[i],0)--point(tr[i],1)--sp--cycle;
  pyrtrfc[nuoftr+1]=point(tr[i],1)--point(tr[i],2)--sp--cycle;
  pyrtrfc[nuoftr+2]=point(tr[i],2)--point(tr[i],0)--sp--cycle;
  nuoftr=nuoftr+3;
 }

for(int j=0;j<24;j=j+1) faces.push(pyrtrfc[j]);
for(int j=0;j<24;j=j+1) filldraw(faces[4*18+j],project(pyrtrfc[j]),orange+yellow,black+2bp);

add(faces);
shipout(defaultfilename,bbox(0.2cm,black,RadialShade(paleblue,darkblue)));

🔗solids-fig015

Author : Jens Schwaiger.
With its pleasant authorization.

Show solids/fig0150.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Polyhedron | #Surface

// PRC/OpenGL version

size(10cm,0);
import graph3;

currentprojection=orthographic(10,3,-2);
// currentlight=nolight;

guide achteck=polygon(8);
real lge=length(point(achteck,1)-point(achteck,0));
int n=8;
guide3[] sq;
guide3[] tr;
triple a,b,c,d;

a=(point(achteck,0).x,point(achteck,0).y,-lge/2);
b=(point(achteck,1).x,point(achteck,1).y,-lge/2);
c=(point(achteck,1).x,point(achteck,1).y,lge/2);
d=(point(achteck,0).x,point(achteck,0).y,lge/2);

sq[0]=a--b--c--d--cycle;
for(int i=1;i<n;i=i+1) sq[i]=rotate(45*i,Z)*sq[0];
for(int i=0;i<3;i=i+1) sq[n+i]=rotate(90,Y)*sq[i];
for(int i=4;i<7;i=i+1) sq[n-1+i]=rotate(90,Y)*sq[i];
for(int i=2;i<3;i=i+1) sq[12+i]=rotate(90,X)*sq[i];
sq[14]=rotate(90,X)*sq[2];
sq[15]=rotate(90,X)*sq[4];
sq[16]=rotate(90,X)*sq[6];
sq[17]=rotate(90,X)*sq[0];

tr[0]=point(sq[2],3)--point(sq[2],2)--point(sq[14],1)--cycle;
for(int i=1;i<4;i=i+1) tr[i]=rotate(90*i,Z)*tr[0];
tr[4]=reverse(point(sq[2],0)--point(sq[2],1)--point(sq[9],2)--cycle);
for(int i=5;i<8;i=i+1) tr[i]=rotate(90*(i-4),Z)*tr[4];

real hgtsq=3;
triple[][][] pyrsq=new triple[18][4][3];
path3[] pyrsqfc=new path3[4*18];
int nofface=0;
for(int i=0;i<18;i=i+1){
  triple cog=0.5(point(sq[i],0)+point(sq[i],2));
  triple sp=cog+
    hgtsq*unit(cross(point(sq[i],1)-point(sq[i],0),point(sq[i],3)-point(sq[i],0)));
  for(int j=0;j<3;j=j+1){
    pyrsq[i][j][0]=point(sq[i],j);
    pyrsq[i][j][1]=point(sq[i],j+1);
    pyrsq[i][j][2]=sp;
    pyrsqfc[nofface]=pyrsq[i][j][0]--pyrsq[i][j][1]--pyrsq[i][j][2]--cycle;
    nofface=nofface+1;
  }
  pyrsq[i][3][0]=point(sq[i],3);
  pyrsq[i][3][1]=point(sq[i],0);
  pyrsq[i][3][2]=sp;
  pyrsqfc[nofface]=pyrsq[i][3][0]--pyrsq[i][3][1]--pyrsq[i][3][2]--cycle;
  nofface=nofface+1;
 }

for(int i=0;i<18*4;i=i+1)
  draw(surface(pyrsqfc[i]),yellow,black+2.5bp);

path3[] pyrtrfc=new path3[3*8];
real hgttr=2;
int nuoftr=0;

for(int i=0;i<8;i=i+1){
  triple cog=(1/3)*(point(tr[i],0)+point(tr[i],1)+point(tr[i],2));
  triple sp=cog+hgttr*unit(cross(point(tr[i],1)-point(tr[i],0),point(tr[i],2)-point(tr[i],0)));
  pyrtrfc[nuoftr]=point(tr[i],0)--point(tr[i],1)--sp--cycle;
  pyrtrfc[nuoftr+1]=point(tr[i],1)--point(tr[i],2)--sp--cycle;
  pyrtrfc[nuoftr+2]=point(tr[i],2)--point(tr[i],0)--sp--cycle;
  nuoftr=nuoftr+3;
 }

for(int j=0;j<24;j=j+1)
  draw(surface(pyrtrfc[j]),orange+yellow,black+2bp);

🔗three-fig001

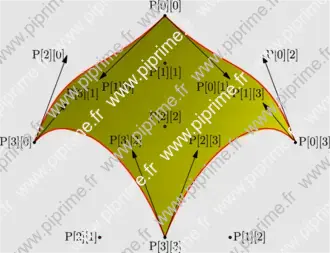
Show three/fig0010.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Direction (3D) | #Patch | #Path3 | #Surface | #Triple

import three;

size(12cm);
currentprojection=orthographic(1,1,1.5);
currentlight=(1,0,1);

triple P00=-X-Y+0.5*Z, P03=-X+Y, P33=X+Y, P30=X-Y;

triple[][] P={
  {P00,P00+(-0.5,0.5,-1),P03+(0,-0.5,1),P03},
  {P00+(0.5,-0.5,-1),(-0.5,-0.5,0.5),(-0.5,0.5,-1.5),P03+(0.5,0,1)},
  {P30+(-0.5,0,1),(0.5,-0.5,-1.5),(0.5,0.5,1),P33+(-0.5,0,1)},
  {P30,P30+(0,0.5,1),P33+(0,-0.5,1),P33}
};

surface s=surface(patch(P));
draw(s,15,15,yellow,meshpen=grey);
draw(sequence(new path3(int i){
      return s.s[i].external();},s.s.length), bp+red);

dot("P[0][0]",P[0][0], align=N, black);
dot("P[0][3]",P[0][3], black);
dot("P[3][3]",P[3][3], align=S, black);
dot("P[3][0]",P[3][0], align=W, black);

draw(Label("P[0][1]",align=SW,EndPoint),P[0][0]--P[0][1], Arrow3);
draw(Label("P[1][0]",align=SE,EndPoint),P[0][0]--P[1][0], Arrow3);

draw(Label("P[0][2]",align=E,EndPoint),P[0][3]--P[0][2], Arrow3);
draw(Label("P[1][3]",EndPoint),P[0][3]--P[1][3], Arrow3);

draw(Label("P[2][3]",EndPoint),P[3][3]--P[2][3], Arrow3);
draw(Label("P[3][2]",EndPoint),P[3][3]--P[3][2], Arrow3);

draw(Label("P[3][1]",EndPoint),P[3][0]--P[3][1], Arrow3);
draw(Label("P[2][0]", align=W,EndPoint),P[3][0]--P[2][0], Arrow3);


dot("P[1][1]",P[1][1], align=S);
dot("P[1][2]",P[1][2], align=E);
dot("P[2][2]",P[2][2], align=N);
dot("P[2][1]",P[2][1], align=W);

for (int i=0; i < s.s.length; ++i)
  dot(s.s[i].internal(), bp+red);

if(!is3D())
  shipout(bbox(Fill(lightgrey)));

🔗three-fig002

Show three/fig0020.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Shading (3D) | #Palette | #Patch | #Path3 | #Surface | #Triple

import three;
import palette;

size(12cm);
currentprojection=orthographic(1,1,1.5);
currentlight=(1,0,1);

triple P00=-X-Y+0.5*Z, P03=-X+Y, P33=X+Y, P30=X-Y;

triple[][] P={
  {P00,P00+(-0.5,0.5,-1),P03+(0,-0.5,1),P03},
  {P00+(0.5,-0.5,-1),(-0.5,-0.5,0.5),(-0.5,0.5,-1.5),P03+(0.5,0,1)},
  {P30+(-0.5,0,1),(0.5,-0.5,-1.5),(0.5,0.5,1),P33+(-0.5,0,1)},
  {P30,P30+(0,0.5,1),P33+(0,-0.5,1),P33}
};

surface s=surface(patch(P));
s.colors(palette(s.map(zpart),Gradient(yellow,red)));
// s.colors(palette(s.map(zpart),Rainbow()));

draw(s);
draw(sequence(new path3(int i){
      return s.s[i].external();},s.s.length), bp+orange);


if(!is3D())
  shipout(bbox(Fill(lightgrey)));

🔗three-fig003

Show three/fig0030.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Shading (3D) | #Palette | #Patch | #Path3 | #Surface | #Triple

import three;

size(10cm);
currentlight=(0,0,1);

surface sf=surface(patch(P=new triple[][] {
      {(0,0,0),(1,0,0),(1,0,0),(2,0,0)},
      {(0,1,0),(1,0,1),(1,0,1),(2,1,0)},
      {(0,1,0),(1,0,-1),(1,0,-1),(2,1,0)},
      {(0,2,0),(1,2,0),(1,2,0),(2,2,0)}
    }));

draw(sf,surfacepen=yellow);
draw(sf.s[0].vequals(0.5),squarecap+2bp+blue,currentlight);
draw(sf.s[0].uequals(0.5),squarecap+2bp+red,currentlight);

🔗three-fig004

Show three/fig0040.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Arrow (3D) | #Triple | #Arc (3D) | #Direction (3D) | #Plan

import three;
size(8cm, 0);
real radius=1, theta=37, phi=60;

currentprojection=perspective(4, 1, 2);

// Planes
pen bg=gray(0.9)+opacity(0.5);
draw(surface((1.2, 0, 0)--(1.2, 0, 1.2)--(0, 0, 1.2)--(0, 0, 0)--cycle), bg, bg);
draw(surface((0, 1.2, 0)--(0, 1.2, 1.2)--(0, 0, 1.2)--(0, 0, 0)--cycle), bg, bg);
draw(surface((1.2, 0, 0)--(1.2, 1.2, 0)--(0, 1.2, 0)--(0, 0, 0)--cycle), bg, bg);

real r=1.5;
draw(Label("$x$", 1), O--r*X, Arrow3(HookHead3));
draw(Label("$y$", 1), O--r*Y, Arrow3(HookHead3));
draw(Label("$z$", 1), O--r*Z, Arrow3(HookHead3));
label("$\rm O$",  (0, 0, 0), W);

triple pQ=radius*dir(theta, phi); // Point Q
// triple pQ=radius*expi(radians(theta), radians(phi)); // Point Q
draw(O--radius*dir(90, phi)^^O--pQ, dashed);
dot("$R*\mathrm{dir}\left(\theta, \phi\right)$", pQ);

// Arcs
draw("$\theta$", reverse(arc(O, 0.5*pQ, 0.5*Z)), N+0.3E, Arrow3(HookHead2));
draw("$\phi$", arc(O, 0.5*X, 0.5*(pQ.x, pQ.y, 0)), N+0.3E, Arrow3(HookHead2));

path3 p3=O--arc(O, radius, 0, phi, 90, phi)--cycle;
draw(surface(p3), blue+opacity(0.5));

🔗three-fig005

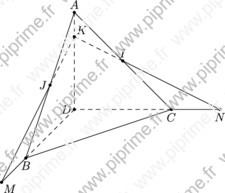
Show three/fig0050.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Geometry (3D) | #Wire frame | #Line type | #Intersection | #Interp

import three; import math;
size(8cm,0);
currentprojection=obliqueX;

real h=2;
triple A =(0,0,h), B=(h,0,0), C=(0,h,0), D=(0,0,0);
triple Ip=midpoint(A--C), J=midpoint(A--B);
triple K=shift((0,0,-0.25*h))*A;

triple M=interp(K,J,intersect(K,J,normal(new triple[]{B,C,D}),D));
triple Np=interp(K,Ip,intersect(K,Ip,normal(new triple[]{B,C,D}),D));

dot("$A$", A, align=Z);  dot("$B$", B, align=S);
dot("$C$", C, align=S);  dot("$D$", D, align=W);
dot("$I$", Ip, align=N); dot("$J$", J, align=W);
dot("$K$", K, align=NE); dot("$M$", M, align=SE);
dot("$N$", Np, align=S);

draw(A--B--C--cycle^^B--M^^C--Np^^J--M^^Ip--Np);
draw(A--D--C^^D--B^^J--K^^K--Ip, dashed);

🔗three-fig006

Show three/fig0060.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Label (3D) | #Projection (3D) | #Plan

settings.render=0;
import three;
size(4cm,0);

currentprojection=perspective((45,45,30));
path3 YZ=plane((0,4,0),(0,0,4));

draw("$x$",project(O--X),Arrow);
draw("$y$",project(O--Y),Arrow);
draw("$z$",project(O--Z),Arrow);
draw(YZ);

label(scale(5)*project("A",Y,Z,(0,1,1)));

🔗three-fig007

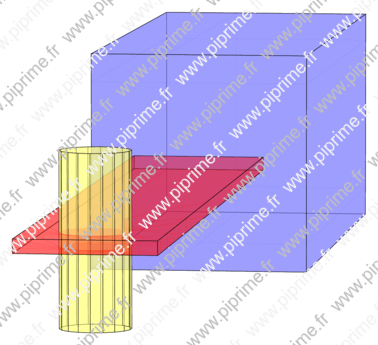
From the Asymptote forum.

Show three/fig0070.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Bsp | #Wire frame | #Plan

import bsp;

typedef path3[] shape;

shape operator *(transform3 T, shape p){
  shape os;
  for(path3 g:p) os.push(T*g);
  return os;
}


path3 path(triple[] T){
  path3 P;
  for(triple i:T) P=P--i;
  return P;
}

void addshapes(face[] F, shape[] shp, pen drawpen=currentpen, pen fillpen=white)
{
  for(int i=0; i < shp.length; ++i)
    for(int j=0; j < shp[i].length; ++j) {
      path3 g=shp[i][j];
      picture pic=F.push(g);
      filldraw(pic, project(g), fillpen, drawpen);
      // filldraw(pic, g, currentlight.intensity(F[F.length-1].point)*fillpen, drawpen);
    }
}

shape cylinder(real R=1, real H=1, int n=18){
  shape Cyl;
  triple[] CTop;
  triple[] CBot;
  for(int i=0; i <= n; ++i)
    CBot.push((R*cos(2pi*i/n), R*sin(2pi*i/n), 0));
  CTop = CBot+(0, 0, H);
  for(int i=0; i < n; ++i)
    Cyl.push(CBot[i]--CBot[i+1]--CTop[i+1]--CTop[i]--cycle);

  path3 P=path(CBot)--cycle;
  Cyl.push(P);
  Cyl.push(shift(H*Z)*P);

  return Cyl;
}

shape rightslab(real x=1, real y=1, real z=1){
  shape slab;
  slab[0] = (0, 0, 0)--(1, 0, 0)--(1, 1, 0)--(0, 1, 0)--cycle;
  slab[1] = (0, 0, 0)--(1, 0, 0)--(1, 0, 1)--(0, 0, 1)--cycle;
  slab[2] = (1, 0, 0)--(1, 1, 0)--(1, 1, 1)--(1, 0, 1)--cycle;
  slab[3] = (1, 1, 0)--(0, 1, 0)--(0, 1, 1)--(1, 1, 1)--cycle;
  slab[4] = (0, 1, 0)--(0, 0, 0)--(0, 0, 1)--(0, 1, 1)--cycle;
  slab[5] = (0, 0, 1)--(1, 0, 1)--(1, 1, 1)--(0, 1, 1)--cycle;
  return scale(x, y, z)*slab;
}

size(10cm, 0);
triple cam=(1600, 200, 150);
//currentprojection=orthographic(1600, 800, 400);
currentprojection=perspective(cam); //Far away!
currentlight=rotate(-45, Z)*(cam+(0, 0, 1000));

real Blen = 180;
real Bwdt = 30;
real Bhgt = 3;
real Clen = 130;
real Cwdt = 50;
real Chgt = 50;
real cylr = 7.5;
real cylh = 37.0 ;

shape slab1 = shift(-Bwdt/2*Y-Bhgt/2*Z+Clen/2*X)*rightslab(Blen, Bwdt, Bhgt);
shape slab2 = shift(-Cwdt/2*Y-Chgt/2*Z-Clen/2*X)*rightslab(Clen, Cwdt, Chgt);
shape cyl1 = shift((Blen+Clen/2-2*cylr)*X-(cylh/2)*Z)*cylinder(R=cylr, H=cylh);

shape[] group1={slab1};
shape[] group2={slab2};
shape[] group3={cyl1};

face[] faces;
addshapes(faces, group1, drawpen=linewidth(0.25bp), fillpen=opacity(0.35)+red);
addshapes(faces, group2, drawpen=linewidth(0.25bp), fillpen=opacity(0.5)+lightblue);
addshapes(faces, group3, drawpen=linewidth(0.25bp), fillpen=opacity(0.5)+lightyellow);
add(faces);

shipout(format="pdf", bbox(3mm, white));

🔗three-fig008

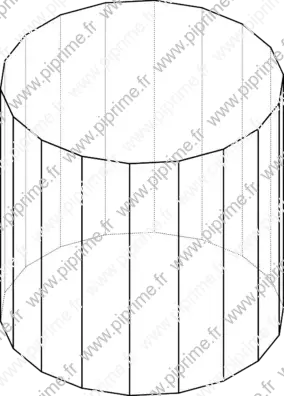
Show three/fig0080.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Bsp | #Wire frame | #Line type | #Plan

import bsp;

typedef path3[] shape;

shape operator *(transform3 T, shape p){
  shape os;
  for(path3 g:p) os.push(T*g);
  return os;
}


path3 path(triple[] T){
  path3 P;
  for(triple i:T) P=P--i;
  return P;
}

void addshapes(face[] F, shape[] shp, pen drawpen=currentpen, pen fillpen=white)
{
  for(int i=0; i < shp.length; ++i)
    for(int j=0; j < shp[i].length; ++j) {
      path3 g=shp[i][j];
      picture pic=F.push(g);
      if(fillpen != nullpen) filldraw(pic,project(g),fillpen, drawpen);
      else draw(pic,project(g),drawpen);
      // filldraw(pic,g,currentlight.intensity(F[F.length-1].point)*fillpen, drawpen);
    }
}

shape cylinder(real R=1, real H=1, int n=18){
  shape Cyl;
  triple[] CTop;
  triple[] CBot;
  for(int i=0; i <= n; ++i)
    CBot.push((R*cos(2pi*i/n), R*sin(2pi*i/n),0));
  CTop = CBot+(0,0,H);
  for(int i=0; i < n; ++i)
    Cyl.push(CBot[i]--CBot[i+1]--CTop[i+1]--CTop[i]--cycle);

  path3 P=path(CBot)--cycle;
  Cyl.push(P);
  Cyl.push(shift(H*Z)*P);

  return Cyl;
}


size(10cm,0);

currentprojection=orthographic(1,1,1);

shape cyl1 = cylinder(R=1, H=2);

shape[] group={cyl1};

face[] hidden, visible;
addshapes(hidden, group, drawpen=linewidth(bp));
addshapes(visible, group, drawpen=dotted, fillpen=nullpen);
add(hidden);
add(visible);

shipout(format="pdf");

🔗three-fig009

Show three/fig0090.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Plan | #Transform (3D) | #Projection (3D) | #Fill/Unfill | #Path3 | #Triple

size(10cm,0);
import three;

currentprojection=obliqueX;

triple v1=(4,0,0),
       v2=(0,6,0),
       p0=(-2,-3,0);
path3 pl1=plane(v1,v2,p0);

path ph=transform(v1,v2,p0,currentprojection)*((0,-2){W}..(0,2){W}..cycle);
filldraw(project(pl1)^^ph,evenodd+lightgrey);

🔗three-fig010

Show three/fig0100.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Plane | #Label (3D) | #Texpath | #Transform (3D) | #Projection (3D) | #Bsp

size(12cm,0);
import bsp;

currentprojection=orthographic(1,1.5,1);

path3 xy=plane((1,0,0),(0,1,0),(0,0,0));
path3 xz=rotate(90,X)*xy;
path3 yz=rotate(-90,Y)*xy;

face[] f;
filldraw(f.push(xy),project(xy),grey);
filldraw(f.push(xz),project(xz),grey);
filldraw(f.push(yz),project(yz),grey);
add(f);

draw(Label("$x$",EndPoint), O--(1,0,0), Arrow3);
draw(Label("$y$",EndPoint), O--(0,1,0), Arrow3);
draw(Label("$z$",EndPoint), O--(0,0,1), Arrow3);
dot(O);

path[] ph=texpath("$\displaystyle\int_{-\infty}^{+\infty}e^{-\alpha x^2}\,dx=
\sqrt{\frac{\pi}{\alpha}}$");
ph =shift((0.5,0.5))*rotate(-45)*scale(1/abs(min(ph)-max(ph)))*ph;

filldraw(project(path3(ph,XYplane)),0.8*yellow);
filldraw(project(path3(ph,ZXplane)),0.8*yellow);
filldraw(project(path3(ph,YZplane)),0.8*yellow);

🔗three-fig011

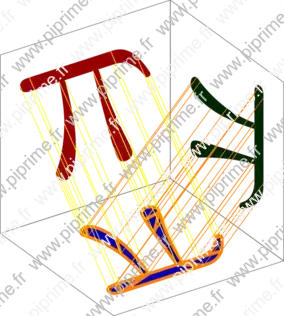
Show three/fig0110.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Plane | #Label (3D) | #Texpath | #Transform (3D) | #Projection (3D)

import three;
size(10cm,0);
currentprojection=orthographic(1,1.5,1);

path3 xy=XY*unitsquare3, xz=ZX*unitsquare3, yz=YZ*unitsquare3;

draw(xy^^xz^^yz, grey);
path3 p3xy=path3(texpath("$\pi$")[0],XYplane);
p3xy=shift((0.5,0.5,0))*scale3(1/abs(min(p3xy)-max(p3xy)))*p3xy;

surface s=surface(p3xy,planar=true);
draw(s, surfacepen=blue, meshpen=orange+3pt);

transform3 Txz=planeproject(xz,(0,-1,1));
draw(Txz*s, red);

transform3 Tyz=planeproject(yz,(-1,0,1));
draw(Tyz*s, green);

path3 p3xz=Txz*p3xy;
path3 p3yz=Tyz*p3xy;

int lg=length(p3xy);
triple p;
for(int i=0;i<=lg;++i) {
  p=point(p3xy,i);
  draw(p--point(p3xz,i), yellow);
  draw(p--point(p3yz,i), orange);
}

🔗tube-fig001

Show tube/fig0010.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
size(12cm,0);

currentprojection=orthographic(0,0.5,1);

// The tube's section used is a path (here an U);
path section=rotate(90)*(N+W--W--E--N+E);

// The tubed curve (yellow tube) has three nodes joined with cubic spline:
path3 p=shift(20X)*scale(10,20,1)*(X..Y..X+Y..cycle);

// A tube is a surface, here the tube is drawn in yellow with purple meshes.
draw(tube(p,section), yellow, bp+purple);
draw(p,red); dot(p);

// The tubed curve (purple tube) has three nodes joined with linear segments:
path3 p=scale(10,20,1)*(X--Y--(X+Y)--cycle);

// Here the tube is drawn in purple with yellow meshes.
draw(tube(p,scale(2)*section), purple, bp+yellow);
draw(p,red); dot(p);

🔗tube-fig002

Show tube/fig0020.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
size(10cm,0);

currentprojection=orthographic(0,0.5,1);
path section=rotate(90)*(N+W--W--E--N+E);

// The tubed curve has three nodes joined with linear segments.
path3 p=scale(10,20,1)*(X--Y--(X+Y)--cycle);

// We may use the routine roundedpath in order to obtain rounded corner:
draw(tube(roundedpath(p,r=0.05),
          section,
          corner=100), // Controls the number of elementary tubes at the corners
     purple, bp+yellow+thin());
draw(p,red); dot(p);

🔗tube-fig003

Show tube/fig0030.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
size(10cm,0);

currentprojection=orthographic(0,0.5,1);
path section=rotate(180)*(N+W--W--E--N+E);

path3 p=scale(5,10,1)*unitcircle3;

draw(tube(p, section,
          relstep=1/6), // Fix the sample step of the relative time (reltime) of the elementary tubes.
     purple, bp+yellow);
draw(p,red); dot(p);

🔗tube-fig004

Show tube/fig0040.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D)

import tube;
import graph3;

size(10cm,0);
currentprojection=perspective(4,3,4);

triple f(real t){
  return t*Z+(cos(2pi*t),sin(2pi*t),0)/sqrt(1+0.5*t^2);
}

path3 p=graph(f,0,2.7,operator ..);
draw(tube(p,scale(0.2)*polygon(5)), purple);

🔗tube-fig005

Show tube/fig0050.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D)

import tube;
import graph3;

size(10cm,0);
currentprojection=perspective(4,3,4);
real x(real t) {return (1/sqrt(1+0.5*t^2))*cos(2pi*t);}
real y(real t) {return (1/sqrt(1+0.5*t^2))*sin(2pi*t);}
real z(real t) {return t;}

path3 p=graph(x,y,z,0,2.7,operator ..);
path section=scale(0.2)*polygon(5);

// tube.asy defines a "colored path".
// The value of coloredtype may be coloredSegments or coloredNodes.
// Here the path scale(0.2)*polygon(5) has fixed colored SEGMENTS.
coloredpath cp=coloredpath(section,
                           // The array of pens become automatically cyclic.
                           new pen[]{0.8*red, 0.8*blue, 0.8*yellow, 0.8*purple, black},
                           colortype=coloredSegments);

// Draw the tube, each SEGMENT of the section is colored.
draw(tube(p,cp));

🔗tube-fig006

Show tube/fig0060.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D)

import tube;
import graph3;

size(10cm,0);
currentprojection=perspective(4,3,4);
real x(real t) {return (1/sqrt(1+0.5*t^2))*cos(2pi*t);}
real y(real t) {return (1/sqrt(1+0.5*t^2))*sin(2pi*t);}
real z(real t) {return t;}

path3 p=graph(x,y,z,0,2.7,operator ..);
path section=scale(0.2)*polygon(5);

// Here the path scale(0.2)*polygon(5) has colored NODES.
coloredpath cp=coloredpath(section,
                           new pen[]{0.8*red, 0.8*blue, 0.8*yellow, 0.8*purple, black},
                           colortype=coloredNodes);

// Draw the tube, each NODE of the section is colored.
draw(tube(p,cp));

🔗tube-fig007

Show tube/fig0070.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D)

import tube;
import graph3;

size(10cm,0);
currentprojection=perspective(4,3,4);
real x(real t) {return (1/sqrt(1+0.5*t^2))*cos(2pi*t);}
real y(real t) {return (1/sqrt(1+0.5*t^2))*sin(2pi*t);}
real z(real t) {return t;}

path3 p=graph(x,y,z,0,2.7,operator ..);
path section=scale(0.2)*polygon(5);

// Define a pen wich depends of a real t. t represent the "reltime" of the path3 p.
pen pen(real t){
  return interp(red,blue,1-2*abs(t-0.5));
}

// Here the section has colored segments (by default) depending to reltime.
draw(tube(p,coloredpath(section,pen)));

🔗tube-fig008

Show tube/fig0080.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D)

import tube;
import graph3;
size(12cm,0);
currentprojection=perspective((-1,1,1));

int p=7, q=3;
real n=p/q;
real a=1, b=1;
real x(real t){return a*cos(t);}
real y(real t){return a*sin(t);}
real z(real t){return b*cos(n*t);}

real R(real t){
  real st2=(n*sin(n*t))^2;
  return a*(1+st2)^(1.5)/sqrt(1+st2+n^4*cos(n*t)^2);
  // return -a*(1+st2)^(1.5)/sqrt(1+st2+n^4*cos(n*t)^2); // Signed radius curvature
}

real mt=q*2*pi;
path3 p=graph(x,y,z,0,mt,operator ..)..cycle;

real m=R(0), M=R(0.5*pi/n);

// Define a pen depending to the radius curvature of graph(x,y,z) at reltime t
pen curvaturePen(real t){
  real r=abs(R(t*mt)-m)/(M-m);
  return interp(red,blue,r);
}

// Draw the tube, colors depend of the radius curvature R.
draw(tube(p,coloredpath(scale(0.1)*unitcircle, curvaturePen)));

🔗tube-fig009

Show tube/fig0090.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D) | #Array

import tube;
import graph3;

size(10cm,0);
currentprojection=perspective(4,3,4);
real x(real t) {return (1/sqrt(1+0.5*t^2))*cos(2pi*t);}
real y(real t) {return (1/sqrt(1+0.5*t^2))*sin(2pi*t);}
real z(real t) {return t;}

path3 p=graph(x,y,z,0,2.7,operator ..);
path section=scale(0.2)*polygon(4);

// Define an array of pen wich depends of a real t. t represent the "reltime" of the path3 p.
pen[] pens(real t){
  return new pen[] {interp(blue,red,t),
      interp(orange,yellow,t),
      interp(green,orange,t),
      interp(red,purple,t)};
}

// "pen[] pens(real t)" allows to color each nodes or segments with a real parameter (the reltime)
// Note that all arrays of pens are convert to cyclical arrays.
draw(tube(p,coloredpath(section,
                        pens,
                        colortype=coloredNodes)));

🔗tube-fig010

Show tube/fig0100.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Transform (3D)

import tube;
import graph3;
size(12cm,0);
currentprojection=orthographic(4,3,2);

real x(real t) {return sin(t);}
real y(real t) {return cos(t);}
real z(real t) {return sqrt(t);}

path3 p=graph(x,y,z,0,4pi,50,operator ..);

path section=subpath(unitcircle,0,2);

pen pens(real t){
  return interp(red,blue,t);
}

// Define a transformation wich will be applied to each section at reltime t.
transform T(real t){return scale(t^0.75/2);}

// Combination of pens and transform:
draw(tube(p,coloredpath(section,pens), T));
draw(p);

🔗tube-fig011

Show tube/fig0110.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
import graph3;
size(12cm,0);
currentprojection=orthographic(4,3,4);

real x(real t) {return sin(t);}
real y(real t) {return 0.5*sin(2*t);}

path g=graph(x,y,0,2pi,50,operator ..);
path3 p=path3(scale(5)*g);

pen pen(real t){
  return interp(red,blue,1-2*abs(t-0.5));
}

draw(tube(p,coloredpath(subpath(unitcircle,1,3),pen)));
draw(p);

🔗tube-fig012

Show tube/fig0120.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Shading (3D)

import tube;
import graph3;
size(12cm,0);
currentprojection=orthographic(1,0,6);

real x(real t) {return sin(t);}
real y(real t) {return 0.5*sin(2*t);}

path g=graph(x,y,0,2pi,50,operator ..);
path3 p=path3(scale(5)*g);

pen[] pens(real t){
  real tt=1-2*abs(t-0.5);
  return new pen[] {interp(red,blue,tt), interp(blue,red,tt)};
}

draw(tube(p,
          coloredpath(polygon(5),pens,colortype=coloredNodes)));
label("colortype=coloredNodes",8*X);

draw(tube(shift(10*Y)*p,
          coloredpath(polygon(5),pens,colortype=coloredSegments)));
label("colortype=coloredSegments",8*X+10Y);

🔗tube-fig013

Show tube/fig0130.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Path | #Graph

import tube;
import graph;
size(12cm,0);
currentprojection=perspective(4,3,6);

real f(real t) {return cos(2*t);}
path g=polargraph(f,0,2pi,10,operator ..)&cycle;
path3 p=path3(scale(20)*g);

draw(tube(p,rotate(60)*polygon(3)), 0.8*red);
draw(tube(shift(Z)*p,scale(0.25)*unitcircle), orange);
draw(shift(1.25*Z)*p);

🔗tube-fig014

Show tube/fig0140.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Path | #Graph

import tube;
import graph;
size(12cm,0);
currentprojection=perspective(0,3,6);

real f(real t) {return cos(2*t);}
path g=polargraph(f,0,2pi,10,operator --)&cycle;
path3 p=path3(scale(20)*g);

draw(tube(p,2W--2E), red, bp+black);
draw(tube(p,unitcircle), orange, bp+black);

🔗tube-fig015

Show tube/fig0150.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
import graph3;
size(12cm,0);
// currentprojection=perspective((2,1,6),-Z); real q=1;
currentprojection=perspective((-1,1,1)); real q=2;

real x(real t){return (1-cos(t))*cos(q*t);}
real y(real t){return (1-cos(t))*sin(q*t);}
real z(real t){return cos(3t);}

path3 p=graph(x,y,z,0,2pi,20,operator ..);
draw(tube(p,scale(0.4,0.1)*unitcircle), purple);

🔗tube-fig016

Show tube/fig0160.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
import graph3;
size(12cm,0);

currentprojection=perspective(1,-1,0);

real x(real t)
{
return 41*cos(t)-18*sin(t)-83*cos(2t)-83*sin(2t)-11*cos(3t)+27*sin(3t);
}

real y(real t)
{
  return 36*cos(t)+27*sin(t)-113*cos(2t)+30*sin(2t)+11*cos(3t)-27*sin(3t);
}

real z(real t)
{
  return 45*sin(t)-30*cos(2t)+113*sin(2t)-11*cos(3t)+27*sin(3t);
}

path3 p=scale3(0.05)*graph(x,y,z,-pi,pi,200,operator --)&cycle;

path section=scale(2,0.5)*unitcircle;
// path section=scale(2,0.5)*polygon(4);
// path section=scale(2)*polygon(6);
draw(tube(p,section), purple);

🔗tube-fig017

Show tube/fig0170.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
import graph3;
size(12cm,0);

currentprojection=perspective(1,-1,0);


path3 p=scale3(20)*randompath3(20,false,operator--)--cycle;

path section=scale(1,0.5)*unitcircle;
// path section=polygon(6);
// path section=scale(1,0.25)*polygon(4);
draw(tube(p,section), purple, bp+yellow);

🔗tube-fig018

Show tube/fig0180.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
import graph3;
size(12cm,0);

currentprojection=perspective(1,-1,0);


path3 p=scale3(20)*randompath3(20,false,operator--)--cycle;

path section=scale(1,0.25)*polygon(4);
draw(tube(roundedpath(p,0.05),section, corner=10), purple);

🔗tube-fig019

Show tube/fig0190.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

import tube;
import solids;

size(12cm,0);
currentprojection=perspective((0,0,1));

int p=8, q=3;
real n=p/q, R=2, r=1;

real x(real t){return (R+r*cos(n*t))*cos(t);}
real y(real t){return (R+r*cos(n*t))*sin(t);}
real z(real t){return r*sin(n*t);}

path3 p=graph(x,y,z,0,6pi,200,operator ..)&cycle;

revolution torus=revolution(Circle(R*X,r,Y,10),Z);

transform T(real t){return scale(0.3+0.25*sin(t*20pi));}

pen[] bpen={0.5red,0.5blue};
bpen.cyclic=true;
pen pen(real t){return bpen[ceil(sin(t*20pi)-1e-3)];}

draw(tube(p,coloredpath(polygon(3),pen),T));
// draw(surface(torus),yellow);

🔗tube-fig020

Show tube/fig0200.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube

// Anneau de Borrommée
// Borromean rings

import tube;
import solids;

size(12cm,0);
currentprojection=perspective((0,0,1));

real a=5, b=2, sq3=sqrt(3);
for (int i=0; i <= 2; ++i) {
  real ai, bi;
  if(i == 0) {
    ai=a/2;
    bi=a*sq3/2;
  } else if(i == 1) {
    ai=-a/2;
    bi=a*sq3/2;
  } else {
    ai=0;
    bi=a*sq3;
  }
  real x(real t){return a*cos(t)+ai;}
  real y(real t){return a*sin(t)+bi;}
  real z(real t){return b*cos(3t);}

  path3 p=graph(x,y,z,0,2pi,100,operator ..)&cycle;


  real trig(real t){return 1-2*abs(t%1-0.5);}
  pen pens(real t) {
    real tt=trig(t+i/3);
    return interp(red,yellow,(tt));
  }

  draw(tube(p, coloredpath(polygon(4),pens)));
}

🔗tube-fig021

Show tube/fig0210.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Palette | #Shading (3D) | #Graph (3D)

import tube;
import graph3;
import palette;

size(12cm,0);
currentprojection=perspective(1,1,1);

int e=1;
real x(real t) {return cos(t)+2*cos(2t);}
real y(real t) {return sin(t)-2*sin(2t);}
real z(real t) {return 2*e*sin(3t);}

path3 p=scale3(2)*graph(x,y,z,0,2pi,50,operator ..)&cycle;

pen[] pens=Rainbow(15);
pens.push(black);
for (int i=pens.length-2; i >= 0 ; --i)
  pens.push(pens[i]);

path sec=subpath(Circle(0,1.5,2*pens.length),0,pens.length);
coloredpath colorsec=coloredpath(sec, pens,colortype=coloredNodes);
draw(tube(p,colorsec));

This page was generated by the Asymptote Exemples Builder
Last modified the 2025-06-30 22:08:01
©2011 Philippe Ivaldi