🔗Asymptote Gallery Tagged by “Revolution” #180
🔗solids-fig001

Show solids/fig0010.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Light (3D) | #Draw (3D) | #Surface | #Sphere | #Revolution | #Projection (3D)
import solids; import three; currentprojection=orthographic(1,2,2); size(6cm,0); material m = material( diffusepen=yellow, emissivepen=black, specularpen=orange, shininess=0.25, metallic=0.5, fresnel0=0.07 ); draw(surface(sphere(1)), m);
🔗solids-fig002

Show solids/fig0020.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Light (3D) | #Draw (3D) | #Surface | #Sphere | #Revolution | #Projection (3D)
import solids; currentlight=light(paleyellow, specularfactor=3, (2,4,6)); size(6cm,0); draw(sphere(1,n=4*nslice), linewidth(bp), m=10); draw(surface(sphere(1,n=4*nslice)), orange);
🔗solids-fig003

Show solids/fig0030.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Revolution | #Projection (3D) | #Draw (3D) | #Surface | #Sphere | #Wire frame | #Line type
// Author: John Bowman. size(6cm, 0); import solids; currentprojection=orthographic(0, 10, 5); nslice=4*nslice; revolution r=sphere(O, 1); draw(surface(r), lightgrey+opacity(0.75)); skeleton s; r.transverse(s, reltime(r.g, 0.6), currentprojection); r.transverse(s, reltime(r.g, 0.5), currentprojection); draw(s.transverse.back, linetype("8 8", 8)); draw(s.transverse.front); r.longitudinal(s, currentprojection); draw(s.longitudinal.front); draw(s.longitudinal.back, linetype("8 8", 8));
🔗solids-fig004

Show solids/fig0040.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Transform (3D) | #Revolution | #Surface | #Sphere | #Projection (3D)
import solids; size(6cm,0); currentprojection=orthographic(100,150,30); real r=1; skeleton s; revolution sph=sphere(O,r); draw(surface(sph), palegray); path3 cle=rotate(90,X)*scale3(r)*unitcircle3; triple cam=unit(currentprojection.camera); real a=degrees(xypart(cam),false)-90; real b=-sgn(cam.z)*aCos(sqrt(cam.x^2+cam.y^2)/abs(cam)); cle=rotate(b,cross(Z,cam))*rotate(a,Z)*cle; draw(cle,4pt+red);
🔗solids-fig005

Show solids/fig0050.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Projection (3D) | #Solid | #Transform (3D) | #Revolution | #Surface | #Sphere | #Light (3D)
import solids; size(6cm,0); currentlight=light(diffuse=yellow, specular=blue, specularfactor=5, (5,-5,10)); // currentprojection=orthographic(100,100,30); real r=2; skeleton s; revolution sph=sphere(O,r); draw(surface(sph),red); triple cam=unit(currentprojection.camera); revolution cle=revolution(O,r*(rotate(90,Z)*cam),cam); draw(cle, 8pt+black);
🔗solids-fig009
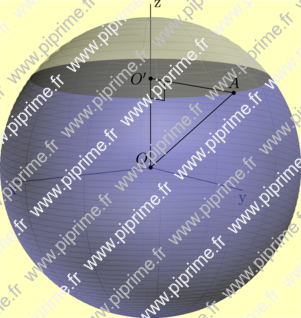
Show solids/fig0090.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Arc (3D) | #Markers | #Revolution | #Surface | #Sphere
size(8cm, 0); import solids; import graph3; //Draw 3D right angle (MA, MB) void drawrightangle(picture pic=currentpicture, triple M, triple A, triple B, real radius=0, pen p=currentpen, pen fillpen=nullpen, projection P=currentprojection) { p=linejoin(0)+linecap(0)+p; if (radius==0) radius=arrowfactor*sqrt(2); transform3 T=shift(-M); triple OA=radius/sqrt(2)*unit(T*A), OB=radius/sqrt(2)*unit(T*B), OC=OA+OB; path3 tp=OA--OC--OB; picture tpic; draw(tpic, tp, p=p); if (fillpen!=nullpen) draw(tpic, surface(O--tp--cycle), fillpen); add(pic, tpic, M); } currentprojection=orthographic(10, 15, 3); real r=10, h=6; // r=sphere radius; h=altitude section triple Op=(0, 0, h); limits((0, 0, 0), 1.1*(r, r, r)); axes3("x", "y", "z"); real rs=sqrt(r^2-h^2); // section radius real ch=180*acos(h/r)/pi; path3 arcD=Arc(O, r, 180, 0, ch, 0, Y, 50); revolution sphereD=revolution(O, arcD, Z); draw(surface(sphereD), opacity(0.5)+lightblue); draw(shift(0, 0, h)*scale3(rs)*surface(unitcircle3), opacity(0.5)); path3 arcU=Arc(O, r, ch, 0, 0, 0, Y, 10); revolution sphereU=revolution(O, arcU, Z); draw(surface(sphereU), opacity(0.33)+lightgrey); // right triangle OO'A triple A=rotate(100, Z)*(rs, 0, h); dot("$O$", O, NW); dot("$O'$", Op, W); dot("$A$", A, N); draw(A--O--Op--A); drawrightangle(Op, O, A); if(!is3D()) shipout(format="pdf", bbox(Fill(paleyellow)));
🔗solids-fig010

Show solids/fig0100.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Revolution | #Wire frame | #Surface
unitsize(1cm); import solids; currentprojection=orthographic(0, 100, 25); real r=4, h=7; triple O=(0, 0, 0); triple Oprime=(0, 0, 3); triple pS=(0, 0, h); triple pA=(r*sqrt(2)/2, r*sqrt(2)/2, 0); revolution rC=cone(O, r, h, axis=Z, n=1); draw(surface(rC), blue+opacity(0.5)); skeleton s; real tOprime=abs(Oprime)/h; rC.transverse(s, reltime(rC.g, tOprime), currentprojection); triple pAprime=relpoint(pA--pS, tOprime); draw(s.transverse.back, dashed); draw(s.transverse.front); label("$S$", pS, N); dot(Label("$O$", align=SE), O); dot(Label("$O'$", align=SE), Oprime); dot(Label("$A$", align=Z), pA); dot(Label("$A'$", align=Z), pAprime); draw(pS--O^^O--pA^^Oprime--pAprime, dashed);
🔗solids-fig011

Show solids/fig0110.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Revolution | #Wire frame | #Sphere
import solids; unitsize(4cm); currentprojection=orthographic(2,2,1); draw(cylinder(c=(0,0,-1.5),r=1,h=3), m=3); draw(sphere(r=1), m=2, frontpen=defaultbackpen);
🔗solids-fig012

Show solids/fig0120.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Intersection | #Revolution | #Wire frame | #Markers
import solids; size(10cm, 0); currentprojection=orthographic(-50, 100, 40); //Draw right angle (MA, MB) in 3D void drawrightangle(picture pic=currentpicture, triple M, triple A, triple B, real radius=0, pen p=currentpen, pen fillpen=nullpen, projection P=currentprojection) { p=linejoin(0)+linecap(0)+p; if (radius==0) radius=arrowfactor*sqrt(2); transform3 T=shift(-M); triple OA=radius/sqrt(2)*unit(T*A), OB=radius/sqrt(2)*unit(T*B), OC=OA+OB; path3 _p=OA--OC--OB; picture pic_; draw(pic_, _p, p=p); if (fillpen!=nullpen) draw(pic_, surface(O--_p--cycle), fillpen); add(pic, pic_, M); } // *...............Construction starts here................* real r=1, h=.75; real gle=60; real gleA=20; transform3 tR=rotate(gle, Z); transform3 tT=shift((0, 0, -h)); triple H=(0, 0, h),//the label is O in the picture. A=rotate(gleA, Z)*(0, r, h), F=tR*A, B=tR*F, D=tT*A, C=tT*B, Ei=intersectionpoint(H--F, A--B); revolution r=cylinder(O, r, h, Z); // draw(surface(r)); draw(r); draw(O--H, dashed); draw(O--D--C--cycle^^O--H^^B--C, dashed); drawrightangle(Ei, H, B, fillpen=black); dot(Label("$O'$", align=invert(NE+E, O)), O); // layer(); draw(surface(A--B--C--D--cycle), lightgrey+opacity(.5)); dot(Label("$A$", align=NW), A); dot(Label("$B$", align=N), B); dot(Label("$C$", align=S), C); dot(Label("$D$", align=NW), D); dot(Label("$E$", align=S), Ei); dot(Label("$F$", align=S), F); dot(Label("$O$", align=N), H); draw(H--B--F--A--cycle^^H--F^^A--B^^A--D);
🔗solids-fig013

Show solids/fig0130.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Label (3D) | #Transform (3D) | #Projection (3D) | #Revolution
import solids; size(8cm,0); currentprojection=orthographic((2, 1, 2)); revolution r=cylinder((0, 0, 0), 1, -10, X); draw(r); draw("$x$",O--X,Arrow3); draw("$y$",O--Y,Arrow3); draw("$z$",O--Z,Arrow3); label(XY()*(scale(2.5)*"This is not a cylinder"), (-5,0,1), align=Z);