Asymptote Gallery Tagged by “Level set (3D)” #159
graph3-fig001

A Möbius strip of half-width with midcircle of radius
and at height can be represented parametrically by :
for in and in . In this parametrization, the Möbius strip is therefore a cubic surface with equation
Source
Show graph3/fig0010.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Surface | #Level set (3D)
import graph3; ngraph=200; size(12cm,0); currentprojection=orthographic(-4,-4,5); real x(real t), y(real t), z(real t); real R=2; void xyzset(real s){ x=new real(real t){return (R+s*cos(t/2))*cos(t);}; y=new real(real t){return (R+s*cos(t/2))*sin(t);}; z=new real(real t){return s*sin(t/2);}; } int n=ngraph; real w=1; real s=-w, st=2w/n; path3 p; triple[][] ts; for (int i=0; i <= n; ++i) { xyzset(s); p=graph(x,y,z,0,2pi); ts.push(new triple[] {}); for (int j=0; j <= ngraph; ++j) { ts[i].push(point(p,j)); } s += st; } pen[] pens={black, yellow, red, yellow, black}; draw(surface(ts, new bool[][]{}), lightgrey); for (int i=0; i <= 4; ++i) { xyzset(-w+i*w/2); draw(graph(x,y,z,0,2pi), 2bp+pens[i]); }
graph3-fig008

Show graph3/fig0080.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Surface | #Level set (3D) | #Contour | #Function (implicit)
// Adapted from the documentation of Asymptote. import graph3; import contour; texpreamble("\usepackage{icomma}"); size3(12cm, 12cm, 8cm, IgnoreAspect); real sinc(pair z) { real r=2pi*abs(z); return r != 0 ? sin(r)/r : 1; } limits((-2, -2, -0.2), (2, 2, 1.2)); currentprojection=orthographic(1, -2, 0.5); xaxis3(rotate(90, X)*"$x$", Bounds(Min, Min), OutTicks(rotate(90, X)*Label, endlabel=false)); yaxis3("$y$", Bounds(Max, Min), InTicks(Label)); zaxis3("$z$", Bounds(Min, Min), OutTicks()); draw(lift(sinc, contour(sinc, (-2, -2), (2, 2), new real[] {0})), bp+0.8*red); draw(surface(sinc, (-2, -2), (2, 2), nx=100, Spline), lightgray); draw(scale3(2*sqrt(2))*unitdisk, paleyellow+opacity(0.25), nolight); draw(scale3(2*sqrt(2))*unitcircle3, 0.8*red);
graph3-fig009
Show graph3/fig0090.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Surface | #Level set (3D) | #Contour | #Function (implicit) | #Palette
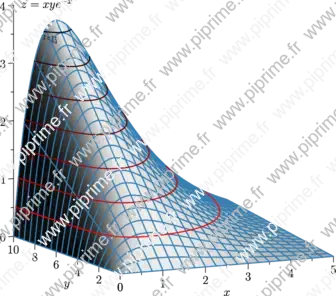
size(12cm,0,false); import graph3; import contour; import palette; texpreamble("\usepackage{icomma}"); real f(pair z) {return z.x*z.y*exp(-z.x);} currentprojection=orthographic(-2.5,-5,1); draw(surface(f,(0,0),(5,10),20,Spline),palegray,bp+rgb(0.2,0.5,0.7)); scale(true); xaxis3(Label("$x$",MidPoint),OutTicks()); yaxis3(Label("$y$",MidPoint),OutTicks(Step=2)); zaxis3(Label("$z=xye^{-x}$",Relative(1),align=2E),Bounds(Min,Max),OutTicks); real[] datumz={0.5,1,1.5,2,2.5,3,3.5}; Label[] L=sequence(new Label(int i) { return YZ()*(Label(format("$z=%g$",datumz[i]), align=2currentprojection.vector()-1.5Z,Relative(1))); },datumz.length); pen fontsize=bp+fontsize(10); draw(L,lift(f,contour(f,(0,0),(5,10),datumz)), palette(datumz,Gradient(fontsize+red,fontsize+black)));
graph3-fig011
Show graph3/fig0110.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
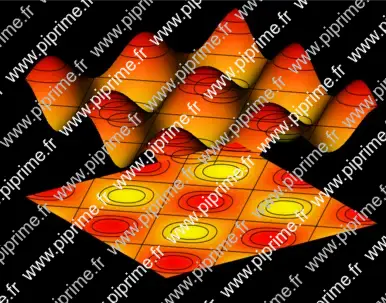
Tags : #Graph (3D) | #Surface | #Level set (3D) | #Contour | #Function (implicit) | #Palette | #Projection (3D) | #Axis (3D) | #Label (3D) | #Shading (3D) | #Shading
import graph3; import palette; import contour; size(14cm,0); currentprojection=orthographic(-1,-1.5,0.75); currentlight=(-1,0,5); real a=1, b=1; real f(pair z) { return a*(6+sin(z.x/b)+sin(z.y/b));} real g(pair z){return f(z)-6a;} // The axes limits((0,0,4a),(14,14,8a)); xaxis3(Label("$x$",MidPoint),OutTicks()); yaxis3(Label("$y$",MidPoint),OutTicks(Step=2)); ticklabel relativelabel() { return new string(real x) {return (string)(x-6a);}; } zaxis3(Label("$z$",Relative(1),align=2E),Bounds(Min,Max),OutTicks(relativelabel())); // The surface surface s=surface(f,(0,0),(14,14),100,Spline); pen[] pens=mean(palette(s.map(zpart),Gradient(yellow,red))); // Draw the surface draw(s,pens); // Project the surface onto the XY plane. draw(planeproject(unitsquare3)*s,pens,nolight); // Draw contour for "datumz" real[] datumz={-1.5, -1, 0, 1, 1.5}; guide[][] pl=contour(g,(0,0),(14,14),datumz); for (int i=0; i < pl.length; ++i) for (int j=0; j < pl[i].length; ++j) draw(path3(pl[i][j])); // Draw the contours on the surface draw(lift(f,pl)); if(!is3D()) shipout(bbox(3mm,Fill(black)));