Asymptote Gallery Tagged by “Shading (3D)” #161
graph3-fig011
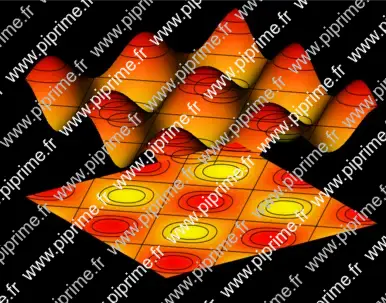
Show graph3/fig0110.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Surface | #Level set (3D) | #Contour | #Function (implicit) | #Palette | #Projection (3D) | #Axis (3D) | #Label (3D) | #Shading (3D) | #Shading
import graph3; import palette; import contour; size(14cm,0); currentprojection=orthographic(-1,-1.5,0.75); currentlight=(-1,0,5); real a=1, b=1; real f(pair z) { return a*(6+sin(z.x/b)+sin(z.y/b));} real g(pair z){return f(z)-6a;} // The axes limits((0,0,4a),(14,14,8a)); xaxis3(Label("$x$",MidPoint),OutTicks()); yaxis3(Label("$y$",MidPoint),OutTicks(Step=2)); ticklabel relativelabel() { return new string(real x) {return (string)(x-6a);}; } zaxis3(Label("$z$",Relative(1),align=2E),Bounds(Min,Max),OutTicks(relativelabel())); // The surface surface s=surface(f,(0,0),(14,14),100,Spline); pen[] pens=mean(palette(s.map(zpart),Gradient(yellow,red))); // Draw the surface draw(s,pens); // Project the surface onto the XY plane. draw(planeproject(unitsquare3)*s,pens,nolight); // Draw contour for "datumz" real[] datumz={-1.5, -1, 0, 1, 1.5}; guide[][] pl=contour(g,(0,0),(14,14),datumz); for (int i=0; i < pl.length; ++i) for (int j=0; j < pl[i].length; ++j) draw(path3(pl[i][j])); // Draw the contours on the surface draw(lift(f,pl)); if(!is3D()) shipout(bbox(3mm,Fill(black)));
graph3-fig012

Show graph3/fig0120.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Projection (3D) | #Shading (3D)
import graph3; import palette; real sinc(real x){return x != 0 ? sin(x)/x : 1;} real f(pair z){ real value = (sinc(pi*z.x)*sinc(pi*z.y))**2; return value^0.25; } currentprojection=orthographic(0,0,1); size(10cm,0); surface s=surface(f,(-5,-5),(5,5),100,Spline); s.colors(palette(s.map(zpart),Gradient((int)2^11 ... new pen[]{black,white}))); draw(planeproject(unitsquare3)*s,nolight);
graph3-fig013

From TeXgraph exemples.
Show graph3/fig0130.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D)
settings.render=0; import graph3; import palette; size(10cm,0); currentprojection=orthographic(2,-2,2.5); real f(pair z) { real u=z.x, v=z.y; return (u/2+v)/(2+cos(u/2)*sin(v)); } surface s=surface(f,(0,0),(14,14),150,Spline); draw(s,mean(palette(s.map(zpart),Gradient(yellow,red)))); if(!is3D()) shipout(bbox(3mm,Fill(black)));
graph3-fig014

From TeXgraph exemples.
Show graph3/fig0140.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D)
settings.render=0; import graph3; import palette; size(15cm,0); currentprojection=orthographic(2,-2,2.5); real f(pair z) { real u=z.x, v=z.y; return (u/2+v)/(2+cos(u/2)*sin(v)); } surface s=surface(f,(0,0),(14,14),50,Spline); s.colors(palette(s.map(zpart),Gradient(yellow,red))); draw(s); if(!is3D()) shipout(bbox(3mm,Fill(black)));
graph3-fig015

Show graph3/fig0150.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D) | #Array | #Spherical harmonics
settings.render=0; import graph3; size(15cm); currentprojection=orthographic(4,2,4); real r(real Theta, real Phi){return 1+0.5*(sin(2*Theta)*sin(2*Phi))^2;} triple f(pair z) {return r(z.x,z.y)*expi(z.x,z.y);} pen[] pens(triple[] z) { return sequence(new pen(int i) { real a=abs(z[i]); return a < 1+1e-3 ? black : interp(blue, red, 2*(a-1)); },z.length); } surface s=surface(f,(0,0),(pi,2pi),100,Spline); // Interpolate the corners, and coloring each patch with one color // produce some artefacts draw(s,pens(s.cornermean())); if(!is3D()) shipout(bbox(3mm,Fill(black)));
graph3-fig016

Show graph3/fig0160.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D) | #Array | #Spherical harmonics
settings.render=0; import graph3; size(15cm); currentprojection=orthographic(4,2,4); real r(real Theta, real Phi){return 1+0.5*(sin(2*Theta)*sin(2*Phi))^2;} triple f(pair z) {return r(z.x,z.y)*expi(z.x,z.y);} pen[][] pens(triple[][] z) { pen[][] p=new pen[z.length][]; for(int i=0; i < z.length; ++i) { triple[] zi=z[i]; p[i]=sequence(new pen(int j) { real a=abs(zi[j]); return a < 1+1e-3 ? black : interp(blue, red, 2*(a-1));}, zi.length); } return p; } surface s=surface(f,(0,0),(pi,2pi),100,Spline); // Here we interpolate the pens, this looks smoother, with fewer artifacts draw(s,mean(pens(s.corners()))); if(!is3D()) shipout(bbox(3mm,Fill(black)));
graph3-fig017

Show graph3/fig0170.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D) | #Array | #Spherical harmonics
import graph3; size(16cm, 0); currentprojection=orthographic(4, 2, 4); real r(real Theta, real Phi){return 1+0.5*(sin(2*Theta)*sin(2*Phi))^2;} triple f(pair z) {return r(z.x, z.y)*expi(z.x, z.y);} pen[][] pens(triple[][] z) { pen[][] p=new pen[z.length][]; for(int i=0; i < z.length; ++i) { triple[] zi=z[i]; p[i]=sequence(new pen(int j) { real a=abs(zi[j]); return a < 1+1e-3 ? black : interp(blue, red, 2*(a-1));}, zi.length); } return p; } surface s=surface(f, (0, 0), (pi, 2pi), 100, Spline); // Here we determine the colors of vertexes (vertex shading). // Since the PRC output format does not support vertex shading of Bezier surfaces, PRC patches // are shaded with the mean of the four vertex colors. s.colors(pens(s.corners())); draw(s); if(!is3D()) shipout(bbox(1mm, Fill(black)));
graph3-fig018

The spherical harmonics are the angular portion of the solution to Laplace's equation in spherical coordinates where azimuthal symmetry is not present.
The spherical harmonics are defined by:
where and is the Legendre polynomial.
Source
Show graph3/fig0180.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Graph3.asy
Tags : #Graph (3D) | #Palette | #Surface | #Shading (3D) | #Spherical harmonics
import palette; import math; import graph3; typedef real fct(real); typedef pair zfct2(real,real); typedef real fct2(real,real); real binomial(real n, real k) { return gamma(n+1)/(gamma(n-k+1)*gamma(k+1)); } real factorial(real n) { return gamma(n+1); } real[] pdiff(real[] p) { // p(x)=p[0]+p[1]x+...p[n]x^n // retourne la dérivée de p real[] dif; for (int i : p.keys) { if(i != 0) dif.push(i*p[i]); } return dif; } real[] pdiff(real[] p, int n) { // p(x)=p[0]+p[1]x+...p[n]x^n // dérivée n-ième de p real[] dif={0}; if(n >= p.length) return dif; dif=p; for (int i=0; i < n; ++i) dif=pdiff(dif); return dif; } fct operator *(real y, fct f) { return new real(real x){return y*f(x);}; } zfct2 operator +(zfct2 f, zfct2 g) {// Défini f+g return new pair(real t, real p){return f(t,p)+g(t,p);}; } zfct2 operator -(zfct2 f, zfct2 g) {// Défini f-g return new pair(real t, real p){return f(t,p)-g(t,p);}; } zfct2 operator /(zfct2 f, real x) {// Défini f/x return new pair(real t, real p){return f(t,p)/x;}; } zfct2 operator *(real x,zfct2 f) {// Défini x*f return new pair(real t, real p){return x*f(t,p);}; } fct fct(real[] p) { // convertit le tableau des coefs du poly p en fonction polynôme return new real(real x){ real y=0; for (int i : p.keys) { y += p[i]*x^i; } return y; }; } real C(int l, int m) { if(m < 0) return 1/C(l,-m); real OC=1; int d=l-m, s=l+m; for (int i=d+1; i <=s ; ++i) OC *= i; return 1/OC; } int csphase=-1; fct P(int l, int m) { // Polynôme de Legendre associé // http://mathworld.wolfram.com/LegendrePolynomial.html if(m < 0) return (-1)^(-m)*C(l,-m)*P(l,-m); real[] xl2; for (int k=0; k <= l; ++k) { xl2.push((-1)^(l-k)*binomial(l,k)); if(k != l) xl2.push(0); } fct dxl2=fct(pdiff(xl2,l+m)); return new real(real x){ return (csphase)^m/(2^l*factorial(l))*(1-x^2)^(m/2)*dxl2(x); }; } zfct2 Y(int l, int m) {// http://fr.wikipedia.org/wiki/Harmonique_sph%C3%A9rique#Expression_des_harmoniques_sph.C3.A9riques_normalis.C3.A9es return new pair(real theta, real phi) { return sqrt((2*l+1)*C(l,m)/(4*pi))*P(l,m)(cos(theta))*expi(m*phi); }; } real xyabs(triple z){return abs(xypart(z));} size(16cm); currentprojection=orthographic(0,1,1); zfct2 Ylm; triple F(pair z) { // real r=0.75+dot(0.25*I,Ylm(z.x,z.y)); // return r*expi(z.x,z.y); real r=abs(Ylm(z.x,z.y))^2; return r*expi(z.x,z.y); } int nb=4; for (int l=0; l < nb; ++l) { for (int m=0; m <= l; ++m) { Ylm=Y(l,m); surface s=surface(F,(0,0),(pi,2pi),60); s.colors(palette(s.map(xyabs),Rainbow())); triple v=(-m,0,-l); draw(shift(v)*s); label("$Y_"+ string(l) + "^" + string(m) + "$:",shift(X/3)*v); } }
solids-fig008

Show solids/fig0080.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Solids.asy
Tags : #Solid | #Plane | #Shading (3D) | #Transform (3D) | #Projection (3D) | #Surface | #Palette
import solids; import palette; size(14cm,0); currentlight=light( gray(0.4), specularfactor=3, (-0.5,-0.25,0.45), (0.5,-0.5,0.5),(0.5,0.5,0.75) ); nslice=4*nslice; surface s=surface(sphere(O,1)); draw(s,lightgrey); path3 pl=plane((1,0,0),(0,1,0),(0,0,-1)); surface pls=shift(3,3,-1e-3)*scale(-6,-6,1)*surface(pl); draw(pls,0.7*red); real dist(triple z){return abs(z-Z);} surface shade; for (int i=0; i < currentlight.position.length; ++i) { shade=planeproject(pl,currentlight.position[i])*s; draw(shade,mean(palette((shade.map(dist)), Gradient(black,gray(0.6)))), nolight); }
three-fig002

Show three/fig0020.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Shading (3D) | #Palette | #Patch | #Path3 | #Surface | #Triple
import three; import palette; size(12cm); currentprojection=orthographic(1,1,1.5); currentlight=(1,0,1); triple P00=-X-Y+0.5*Z, P03=-X+Y, P33=X+Y, P30=X-Y; triple[][] P={ {P00,P00+(-0.5,0.5,-1),P03+(0,-0.5,1),P03}, {P00+(0.5,-0.5,-1),(-0.5,-0.5,0.5),(-0.5,0.5,-1.5),P03+(0.5,0,1)}, {P30+(-0.5,0,1),(0.5,-0.5,-1.5),(0.5,0.5,1),P33+(-0.5,0,1)}, {P30,P30+(0,0.5,1),P33+(0,-0.5,1),P33} }; surface s=surface(patch(P)); s.colors(palette(s.map(zpart),Gradient(yellow,red))); // s.colors(palette(s.map(zpart),Rainbow())); draw(s); draw(sequence(new path3(int i){ return s.s[i].external();},s.s.length), bp+orange); if(!is3D()) shipout(bbox(Fill(lightgrey)));
three-fig003

Show three/fig0030.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Three.asy
Tags : #Shading (3D) | #Palette | #Patch | #Path3 | #Surface | #Triple
import three; size(10cm); currentlight=(0,0,1); surface sf=surface(patch(P=new triple[][] { {(0,0,0),(1,0,0),(1,0,0),(2,0,0)}, {(0,1,0),(1,0,1),(1,0,1),(2,1,0)}, {(0,1,0),(1,0,-1),(1,0,-1),(2,1,0)}, {(0,2,0),(1,2,0),(1,2,0),(2,2,0)} })); draw(sf,surfacepen=yellow); draw(sf.s[0].vequals(0.5),squarecap+2bp+blue,currentlight); draw(sf.s[0].uequals(0.5),squarecap+2bp+red,currentlight);
tube-fig005

Show tube/fig0050.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D)
import tube; import graph3; size(10cm,0); currentprojection=perspective(4,3,4); real x(real t) {return (1/sqrt(1+0.5*t^2))*cos(2pi*t);} real y(real t) {return (1/sqrt(1+0.5*t^2))*sin(2pi*t);} real z(real t) {return t;} path3 p=graph(x,y,z,0,2.7,operator ..); path section=scale(0.2)*polygon(5); // tube.asy defines a "colored path". // The value of coloredtype may be coloredSegments or coloredNodes. // Here the path scale(0.2)*polygon(5) has fixed colored SEGMENTS. coloredpath cp=coloredpath(section, // The array of pens become automatically cyclic. new pen[]{0.8*red, 0.8*blue, 0.8*yellow, 0.8*purple, black}, colortype=coloredSegments); // Draw the tube, each SEGMENT of the section is colored. draw(tube(p,cp));
tube-fig006

Show tube/fig0060.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D)
import tube; import graph3; size(10cm,0); currentprojection=perspective(4,3,4); real x(real t) {return (1/sqrt(1+0.5*t^2))*cos(2pi*t);} real y(real t) {return (1/sqrt(1+0.5*t^2))*sin(2pi*t);} real z(real t) {return t;} path3 p=graph(x,y,z,0,2.7,operator ..); path section=scale(0.2)*polygon(5); // Here the path scale(0.2)*polygon(5) has colored NODES. coloredpath cp=coloredpath(section, new pen[]{0.8*red, 0.8*blue, 0.8*yellow, 0.8*purple, black}, colortype=coloredNodes); // Draw the tube, each NODE of the section is colored. draw(tube(p,cp));
tube-fig007

Show tube/fig0070.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D)
import tube; import graph3; size(10cm,0); currentprojection=perspective(4,3,4); real x(real t) {return (1/sqrt(1+0.5*t^2))*cos(2pi*t);} real y(real t) {return (1/sqrt(1+0.5*t^2))*sin(2pi*t);} real z(real t) {return t;} path3 p=graph(x,y,z,0,2.7,operator ..); path section=scale(0.2)*polygon(5); // Define a pen wich depends of a real t. t represent the "reltime" of the path3 p. pen pen(real t){ return interp(red,blue,1-2*abs(t-0.5)); } // Here the section has colored segments (by default) depending to reltime. draw(tube(p,coloredpath(section,pen)));
tube-fig008

Show tube/fig0080.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D)
import tube; import graph3; size(12cm,0); currentprojection=perspective((-1,1,1)); int p=7, q=3; real n=p/q; real a=1, b=1; real x(real t){return a*cos(t);} real y(real t){return a*sin(t);} real z(real t){return b*cos(n*t);} real R(real t){ real st2=(n*sin(n*t))^2; return a*(1+st2)^(1.5)/sqrt(1+st2+n^4*cos(n*t)^2); // return -a*(1+st2)^(1.5)/sqrt(1+st2+n^4*cos(n*t)^2); // Signed radius curvature } real mt=q*2*pi; path3 p=graph(x,y,z,0,mt,operator ..)..cycle; real m=R(0), M=R(0.5*pi/n); // Define a pen depending to the radius curvature of graph(x,y,z) at reltime t pen curvaturePen(real t){ real r=abs(R(t*mt)-m)/(M-m); return interp(red,blue,r); } // Draw the tube, colors depend of the radius curvature R. draw(tube(p,coloredpath(scale(0.1)*unitcircle, curvaturePen)));
tube-fig009

Show tube/fig0090.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Graph (3D) | #Shading (3D) | #Array
import tube; import graph3; size(10cm,0); currentprojection=perspective(4,3,4); real x(real t) {return (1/sqrt(1+0.5*t^2))*cos(2pi*t);} real y(real t) {return (1/sqrt(1+0.5*t^2))*sin(2pi*t);} real z(real t) {return t;} path3 p=graph(x,y,z,0,2.7,operator ..); path section=scale(0.2)*polygon(4); // Define an array of pen wich depends of a real t. t represent the "reltime" of the path3 p. pen[] pens(real t){ return new pen[] {interp(blue,red,t), interp(orange,yellow,t), interp(green,orange,t), interp(red,purple,t)}; } // "pen[] pens(real t)" allows to color each nodes or segments with a real parameter (the reltime) // Note that all arrays of pens are convert to cyclical arrays. draw(tube(p,coloredpath(section, pens, colortype=coloredNodes)));
tube-fig012

Show tube/fig0120.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Shading (3D)
import tube; import graph3; size(12cm,0); currentprojection=orthographic(1,0,6); real x(real t) {return sin(t);} real y(real t) {return 0.5*sin(2*t);} path g=graph(x,y,0,2pi,50,operator ..); path3 p=path3(scale(5)*g); pen[] pens(real t){ real tt=1-2*abs(t-0.5); return new pen[] {interp(red,blue,tt), interp(blue,red,tt)}; } draw(tube(p, coloredpath(polygon(5),pens,colortype=coloredNodes))); label("colortype=coloredNodes",8*X); draw(tube(shift(10*Y)*p, coloredpath(polygon(5),pens,colortype=coloredSegments))); label("colortype=coloredSegments",8*X+10Y);
tube-fig021

Show tube/fig0210.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 3D | Tube.asy
Tags : #Tube | #Palette | #Shading (3D) | #Graph (3D)
import tube; import graph3; import palette; size(12cm,0); currentprojection=perspective(1,1,1); int e=1; real x(real t) {return cos(t)+2*cos(2t);} real y(real t) {return sin(t)-2*sin(2t);} real z(real t) {return 2*e*sin(3t);} path3 p=scale3(2)*graph(x,y,z,0,2pi,50,operator ..)&cycle; pen[] pens=Rainbow(15); pens.push(black); for (int i=pens.length-2; i >= 0 ; --i) pens.push(pens[i]); path sec=subpath(Circle(0,1.5,2*pens.length),0,pens.length); coloredpath colorsec=coloredpath(sec, pens,colortype=coloredNodes); draw(tube(p,colorsec));