Tag Arc (3D) -- Asymptote Gallery

🔗Asymptote Gallery Tagged by “Arc (3D)” #177

🔗solids-fig009

Figure solids 009 Generated with Asymptote

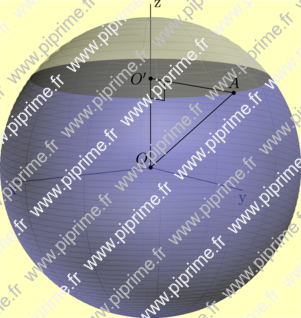
size(8cm, 0);
import solids;
import graph3;

//Draw 3D right angle (MA, MB)
void drawrightangle(picture pic=currentpicture,
                    triple M, triple A, triple B,
                    real radius=0,
                    pen p=currentpen,
                    pen fillpen=nullpen,
                    projection P=currentprojection)
{
  p=linejoin(0)+linecap(0)+p;
  if (radius==0) radius=arrowfactor*sqrt(2);
  transform3 T=shift(-M);
  triple OA=radius/sqrt(2)*unit(T*A),
    OB=radius/sqrt(2)*unit(T*B),
    OC=OA+OB;
  path3 tp=OA--OC--OB;
  picture tpic;
  draw(tpic, tp, p=p);
  if (fillpen!=nullpen) draw(tpic, surface(O--tp--cycle), fillpen);
  add(pic, tpic, M);
}

currentprojection=orthographic(10, 15, 3);

real r=10, h=6; // r=sphere radius; h=altitude section
triple Op=(0, 0, h);

limits((0, 0, 0), 1.1*(r, r, r));
axes3("x", "y", "z");

real rs=sqrt(r^2-h^2); // section radius
real ch=180*acos(h/r)/pi;
path3 arcD=Arc(O, r, 180, 0, ch, 0, Y, 50);

revolution sphereD=revolution(O, arcD, Z);
draw(surface(sphereD), opacity(0.5)+lightblue);
draw(shift(0, 0, h)*scale3(rs)*surface(unitcircle3), opacity(0.5));

path3 arcU=Arc(O, r, ch, 0, 0, 0, Y, 10);
revolution sphereU=revolution(O, arcU, Z);
draw(surface(sphereU), opacity(0.33)+lightgrey);

// right triangle OO'A
triple A=rotate(100, Z)*(rs, 0, h);
dot("$O$", O, NW);
dot("$O'$", Op, W);
dot("$A$", A, N);
draw(A--O--Op--A);
drawrightangle(Op, O, A);

if(!is3D())
  shipout(format="pdf", bbox(Fill(paleyellow)));

🔗three-fig004

Figure three 004 Generated with Asymptote

import three;
size(8cm, 0);
real radius=1, theta=37, phi=60;

currentprojection=perspective(4, 1, 2);

// Planes
pen bg=gray(0.9)+opacity(0.5);
draw(surface((1.2, 0, 0)--(1.2, 0, 1.2)--(0, 0, 1.2)--(0, 0, 0)--cycle), bg, bg);
draw(surface((0, 1.2, 0)--(0, 1.2, 1.2)--(0, 0, 1.2)--(0, 0, 0)--cycle), bg, bg);
draw(surface((1.2, 0, 0)--(1.2, 1.2, 0)--(0, 1.2, 0)--(0, 0, 0)--cycle), bg, bg);

real r=1.5;
draw(Label("$x$", 1), O--r*X, Arrow3(HookHead3));
draw(Label("$y$", 1), O--r*Y, Arrow3(HookHead3));
draw(Label("$z$", 1), O--r*Z, Arrow3(HookHead3));
label("$\rm O$",  (0, 0, 0), W);

triple pQ=radius*dir(theta, phi); // Point Q
// triple pQ=radius*expi(radians(theta), radians(phi)); // Point Q
draw(O--radius*dir(90, phi)^^O--pQ, dashed);
dot("$R*\mathrm{dir}\left(\theta, \phi\right)$", pQ);

// Arcs
draw("$\theta$", reverse(arc(O, 0.5*pQ, 0.5*Z)), N+0.3E, Arrow3(HookHead2));
draw("$\phi$", arc(O, 0.5*X, 0.5*(pQ.x, pQ.y, 0)), N+0.3E, Arrow3(HookHead2));

path3 p3=O--arc(O, radius, 0, phi, 90, phi)--cycle;
draw(surface(p3), blue+opacity(0.5));