PIPRIME.FR BLOG

Live fully to honor life

Tag Clip -- Asymptote Gallery

đź”—geometry-fig028

Figure geometry 028 Generated with Asymptote

Show geometry/fig0280.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Geometry.asy
Tags : #Geometry | #Point | #Clip | #Circle

import geometry;
size(10cm);

// currentcoordsys=cartesiansystem((2,1),i=(1,0.5),j=(-0.25,0.75));
// show(currentcoordsys);

point A=(-1,0), B=(2,0), C=(0,2);

draw(line(A,B), linewidth(bp));
draw(line(A,C), linewidth(bp));
draw(line(B,C), linewidth(bp));

/*<asyxml><view file="modules/geometry.asy" type="circle" signature="circle(point,point,point)"/></asyxml>*/
circle cc=circle(A,B,C);
draw(cc, blue);
dot(cc.C, blue);

/*<asyxml><view file="modules/geometry.asy" type="circle" signature="incircle(point,point,point)"/></asyxml>*/
circle ic=incircle(A,B,C);
draw(ic, red);
dot(ic.C, red);


/*<asyxml><view file="modules/geometry.asy" type="circle" signature="excircle(point,point,point)"/></asyxml>*/
circle ec=excircle(A,B,C);
/*<asyxml><view file="modules/geometry.asy" type="void" signature="clipdraw(picture,Label,path,align,pen,arrowbar,arrowbar,real,real,Label,marker)"/></asyxml>*/
clipdraw(ec, green);
dot(ec.C, green);

ec=excircle(A,C,B);
clipdraw(ec, green);
dot(ec.C, green);

ec=excircle(C,B,A);
clipdraw(ec, green);
dot(ec.C, green);

dot("G",centroid(A,B,C),NE);

// Enlarge the bounding box of the current picture
// draw(box((-2.5,-3), (3.5,3.5)));

đź”—geometry-fig033

Figure geometry 033 Generated with Asymptote

Show geometry/fig0330.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Geometry.asy
Tags : #Geometry | #Draw (2D) | #Clip | #Deferred drawing | #Parabola

import geometry;
size(10cm);

point F=(2,-1.5);
dot("$F$",F,N,red);

// Enlarge the bounding box of the current picture.
draw(box((-1,-1),(3,1.5)),dashed);//,invisible);

parabola p=parabola(F,0.2,90);

// Define the bounding box to draw the parabola.
// Try finalbounds(); to determine the final bounding box.
p.bmin=(-0.75,-0.4);
p.bmax=(2.75,0.75);

draw(box(p.bmin,p.bmax),red);

draw(p,dashed);/* Defered drawing to adjust the path to the final
                  bounding box.*/

draw((path)p,red); /* The path of 'p' is restricted to the box whose
                  the corners are p.bmin, p.bmax.*/

đź”—geometry-fig034

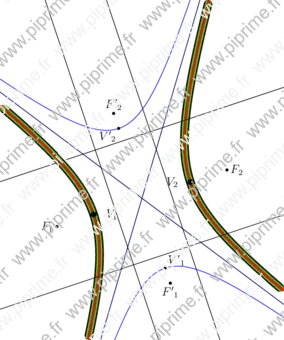
Figure geometry 034 Generated with Asymptote

Show geometry/fig0340.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Examples 2D | Geometry.asy
Tags : #Geometry | #Draw (2D) | #Clip | #Deferred drawing | #Hyperbola | #Line

import geometry;
size(10cm,0);

// currentcoordsys=cartesiansystem((2,1),i=(1,0.5),j=(-0.25,.75));
// show(currentcoordsys);

point F1=(1,0);
point F2=(4,1);
dot("$F_1$",F1,W);
dot("$F_2$",F2);

// Enlarge the bounding box of the current picture
draw(box((0,-2), (5,4)), invisible);

/*<asyxml><view file="modules/geometry.asy" type="hyperbola" signature="hyperbola(point,point,real,bool)"/></asyxml>*/
hyperbola h=hyperbola(F1, F2, 0.9);
draw(h, linewidth(3mm));
draw(h.A1, grey);
draw(h.A2, grey);
draw(h.D1);
draw(h.D2);

/*<asyxml><view file="modules/geometry.asy" type="hyperbola" signature="hyperbola(point,real,real,real)"/></asyxml>*/
draw(hyperbola(h.C, h.a, h.b, h.angle), 2mm+green);

/*<asyxml><view file="modules/geometry.asy" type="hyperbola" signature="hyperbola(bqe)"/></asyxml>*/
draw(hyperbola(equation(h)), 1mm+red);

/*<asyxml><view file="modules/geometry.asy" type="hyperbola" signature="conj(hyperbola)"/></asyxml>*/
hyperbola ch=conj(h);
draw(ch, blue);
draw(ch.A1, 0.5blue);
draw(ch.A2, 0.5blue);
draw(ch.D1);
draw(ch.D2);
dot("${V'}_1$", ch.V1, NE);
dot("${V'}_2$", ch.V2, SW);
dot("${F'}_1$", ch.F1, S);
dot("${F'}_2$", ch.F2, N);

dot("$V_1$", h.V1, 2E, linewidth(2mm));
dot("$V_2$", h.V2, 2W, linewidth(2mm));

đź”—tiling-fig002

Figure tiling 002 Generated with Asymptote

Show tiling/fig0020.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Surveys | Tiling
Tags : #Tiling | #Clip

size(6cm,0);

//Circular paving with the unit hexagonal picture "hexa"
picture pavehexagonal(picture hexa, int depth=1)
{
  picture opic;
  pair center;
  real a,ap,r,rp,r_d=180/pi;

  add(opic, hexa);

  for(int j=0; j<depth; ++j)
    {
      for (int i=1; i<=6; ++i)
	{
	  a=i*60-30;
	  r=j*sqrt(3);
	  center=r*(rotate(a)*(1,0));
	  add(opic, shift(center)*hexa);
	  rp=r;
	  ap=0;
	  for (real k=0; k<j-1; ++k)
	    {
	      r=sqrt((1.5*(j-1 - k))^2 + 3/4*(j+1 + k)^2);
	      ap+=r_d*acos((rp^2 + r^2 - 3)/(2*r*rp));
	      center=r*(rotate(a + ap)*(1,0));
	      add(opic, shift(center)*hexa);
	      rp=r;
	    }
	}
    }
  return opic;
}

picture hexa;
fill(hexa, polygon(6));
path inh=(0,0)--(.6,sqrt(3)/4)--(.5,sqrt(3)/2)--cycle;

for(int i=0; i<6; ++i)
  {
    fill(hexa, rotate(60*i)*inh,.5red);
  }

draw(hexa, inh);
add(rotate(45)*pavehexagonal(hexa,10));
clip(scale(10)*shift(-.5,-.5)*unitsquare);

đź”—tiling-fig006

Figure tiling 006 Generated with Asymptote

Show tiling/fig0060.asy on Github.
Generated with Asymptote 3.00-0.
Categories : Surveys | Tiling
Tags : #Tiling | #Clip

size(10cm,0);

transform r60=rotate(60);

pair A=(1,0);
pair B=r60*A, C=r60*B, D=r60*C, E=r60*D, F=r60*E;

real ad=30;
real tensio=.25;
path AB=A {dir(120-ad)} .. shift(tensio*dir(30))*midpoint(A--B)  .. B {dir(120+ad)};
path BC=reverse(rotate(240,B)*AB);
path CD=reverse(rotate(240,C)*BC);
path DE=reverse(rotate(240,D)*CD);
path EF=reverse(rotate(240,E)*DE);
path FA=reverse(rotate(240,F)*EF);
path pth1=AB--BC--CD--DE--EF--FA;

real tensio=.5;
path AB=A {dir(120-ad)} .. shift(tensio*dir(30))*midpoint(A--B)  .. B {dir(120+ad)};
path BC=reverse(rotate(240,B)*AB);
path CD=reverse(rotate(240,C)*BC);
path DE=reverse(rotate(240,D)*CD);
path EF=reverse(rotate(240,E)*DE);
path FA=reverse(rotate(240,F)*EF);
path pth2=AB--BC--CD--DE--EF--FA;


//Circular paving with the unit hexagonal picture "hexa"
picture pavehexagonal(picture hexa, int depth=1)
{
  picture opic;
  pair center;
  real a,ap,r,rp,r_d=180/pi;

  add(opic, hexa);

  for(int j=0; j<depth; ++j)
    {
      for (int i=1; i<=6; ++i)
 {
   a=i*60-30;
   r=j*sqrt(3);
   center=r*(rotate(a)*(1,0));
   add(opic, shift(center)*hexa);
   rp=r;
   ap=0;
   for (real k=0; k<j-1; ++k)
     {
       r=sqrt((1.5*(j-1 - k))^2 + 3/4*(j+1 + k)^2);
       ap+=r_d*acos((rp^2 + r^2 - 3)/(2*r*rp));
       center=r*(rotate(a + ap)*(1,0));
       add(opic, shift(center)*hexa);
       rp=r;
     }
 }
    }
  return opic;
}

picture hexa, hexat;

real lux=-.3, sq=sqrt(3);
radialshade(hexa,pth1--cycle,
	    lightgrey,(lux*sq/2,lux/2),0,
	    grey,(lux*sq/2,lux/2),1+abs(lux));


add(hexat,scale(1/(3*sq))*pavehexagonal(hexa,5));
clip(hexat,pth2--cycle);
draw(hexat,pth2);
add(pavehexagonal(hexat,4));

This page was generated by the Asymptote Exemples Builder
Last modified the 2025-06-30 22:08:01
©2011 Philippe Ivaldi

0%